One, two, three, let's do it
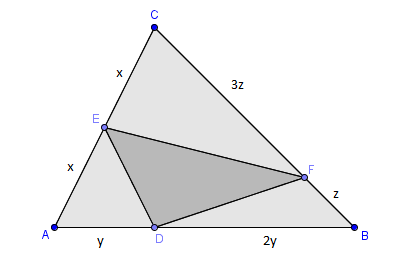 In the diagram, relative lengths of some line segments are as follows:
In the diagram, relative lengths of some line segments are as follows:
C E = A E , D B = 2 A D , C F = 3 B F .
If the area of △ A B C is 2 4 , what is the area of △ D E F ?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Nice question and solution, Paola. I think that you meant C E = A E as one of the written conditions, to be consistent with the diagram. :)
That solution is damn awesome!!
No trig needed here. Use similar triangles to compare base and height of each portion.
Log in to reply
You are right! but it is easier solve it by trig
HOW by similiraity ? This problem made me feel like an idiot :3
Exactly what I did :)
this solution is unpredictable for me its amazing
Answer is as beautiful as you......
Where I can write solution I have more easy solution then this
Log in to reply
Between the question and Paola's solution is a box titled "Add your own solution". Good new solutions are always welcome. :)
There is a typo error in column 1 - third row. ADE must be FCE.
We know that area of triangle is directly proportional to its base and height.
Since △ B D F has a base 3 2 and height 4 1 of those of △ A B C , the area of △ B D F = 3 2 × 4 1 × 2 4 = 4 .
Similarly, the area of △ A D E = 3 1 × 2 1 × 2 4 = 4 .
And, the area of △ C E F = 2 1 × 4 3 × 2 4 = 9 .
Therefore, the area of △ D E F = 2 4 − 4 − 4 − 9 = 7 .
we can see that side of triangle bde has a base 2/3 but what about height it is not given that the angle is 90 degree.. plz tell
Log in to reply
Yes, Danish Mohammed is right. Altitudes from C and F to base AB is proportional to sides FB and CB. If you draw parallel lines through C and F perpendicular to the altitudes you can easily see it. Therefore, the height of △ B D F is z + 3 z z that of △ A B C .
Log in to reply
Woow! :D U r a genius ^_^ Thanks , I spent days to understand this :'D
how to get area triangle CEF ? how to get a relation between its height and the height of the triangle ABC
Looking at triangle BDF, I see how the base is 2/3 of side AB, but I can't see how the height is 1/4? Side BF is 1/4 of BC, so how can the height be 1/4? Sorry, still confused. :(
Log in to reply
From C drop a perpendicular to B A . Let it intersect B A at M . Now from F draw a line parallel to A B intersecting the perpendicular C M at at (say) N . Notice that N M has the same measure as the height of Δ B F D . Now we have a triangle Δ M C B with the line N F parallel to its base B M . From the Intercept Theorem, we have C M N M = C B B F = 4 z z = 4 1
And this implies that N M = 4 1 C M and since C M is a height of Δ A C B , we know now that the height of Δ B F D is 1 / 4 of the height of Δ A C B
See the reply of Danish Mohammed and mine.
My solution uses some heavy machinery to crack a not very tough nut. I hope you like it!
I will use pairs of letters to stand for vectors in the obvious way. Then the required area in terms of the vector cross product is
△ D E F = 2 1 ∣ D E × D F ∣
⟹ △ D E F = 2 1 ∣ ∣ ∣ ∣ ( 3 1 B A + 2 1 A C ) × ( 3 2 A B + 4 1 B C ) ∣ ∣ ∣ ∣
now remembering that the vector product of parallel vectors is zero, and recognising that A C × B C = C A × C B
△ D E F = 2 1 ∣ ∣ ∣ ∣ 1 2 1 B A × B C + 3 1 A C × A B + 8 1 C A × C B ∣ ∣ ∣ ∣
Now the cross products are all perpendicular to the plane of the paper, and the magnitude of each of the cross products is twice the area of the original triangle. But by the right hand rule you can see that the last term points in the opposite direction to the first two. So the above expression becomes
= 2 2 × 2 4 ∣ ∣ ∣ ∣ 1 2 1 + 3 1 − 8 1 ∣ ∣ ∣ ∣
= ∣ 2 + 8 − 3 ∣ = 7
Well you made the problem look like a monster!
Very heavy machinery!!
P.s. Great solution anyways
There exists an area-preserving linear transformation T that maps the triangle ABC into the triangle (0,0), (6,0), and (0,8), with area 24, and the triangle DEF into (3,4), (0,2), and (4,0), with area 7
Let θ = ∠ C A B , β = ∠ A C B and ϕ = ∠ A B C . We have
2 4 = 2 1 ( 3 y ) ( 2 x ) ( sin θ ) ⟹ x y sin θ = 8
A [ A E D ] = 2 1 x y sin θ = 2 1 ( 8 ) = 4
2 4 = 2 1 ( 2 x ) ( 4 z ) ( sin β ) ⟹ x z sin β = 6
A [ E C F ] = 2 1 ( x ) ( 3 z ) ( sin β ) = 2 3 ( 6 ) = 9
2 4 = 2 1 ( 3 y ) ( 4 z ) ( sin ϕ ) ⟹ y z sin ϕ = 4
A [ F B D ] = 2 1 ( z ) ( 2 y ) ( sin ϕ ) = z y sin ϕ = 4
Therefore,
A [ D E F ] = 2 4 − A [ A E D ] − A [ E C F ] − A [ F B D ] = 2 4 − 4 − 9 − 4 = 7
Take a special case: use right triangle with sides 6 , 8 , 1 0 whose area is 2 4
Configure the lengths of the divided segments. This gives 4 triangles: 1 smaller right triangle, and 3 scalene triangles including the one we're looking for.
Draw the altitudes of the 2 scalene triangle so (excluding the one we're asked to find). This forms even smaller right triangles inside the scalene triangles. Use right triangle proportions to find the lengths of the altitudes. Find the area of the 2 scalene triangles and the small right triangle, add them up and subtract the sum from 24 and you'll get 7
Add a dot G in the middle of C and B. Dot G will be 2 z from C and D, and line EG will be parallel to AB. AC is twice the length of CE, so the area of ABC is 4 times of CEG, so we know that CEG is 6 and AEGB will be 1 8 . EG will be half of AB, which is 3 y / 2 . Assume the distance between EG and AB to be d , area AEGB will be the area sum of triangle AEB and EGB 3 yd / 2 + 3 yd / 4 = 1 8 . we can find that yd / 2 = 4 , AED and DFB will be 4 ,EGF will be 3 . Subtract all and EFD will be \boxed{7}.
peasant's solution:
1. Make the given triangle an isosceles right triangle with vertices at (0,0) (0,4sqrt3) and (4sqrt3,0)
2. Using analytic geometry, the vertices of triangle DEF are (0,2sqrt3) (4qrt3 / 3, 0) and (3sqrt3, sqrt3)
3. Then use the formula for solving area of triangle given three vertices (determinant method)
Using the formula Area = 2 1 a b sin C we get:
∴ the area of △ D E F is 1 − 2 4 1 7 = 2 4 7 from △ A B C so △ D E F area is 7