One Well That Ends Well
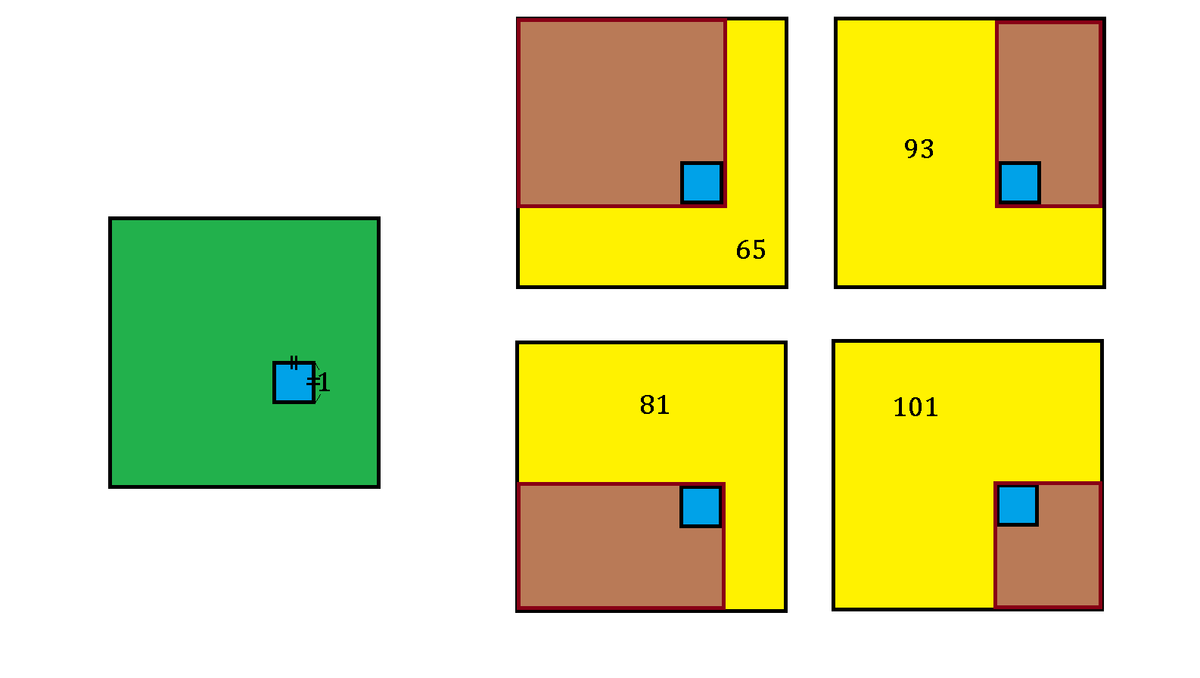
A landlord is surveying his square field that has a well of square area of 1 × 1 m 2 situated somewhere, and its sides are parallel to those of the field, as shown above.
After measuring the landscape, the landlord designs 4 different diagrams to keep his cattle within the (brown) rectangular areas, involving the well, and the L-shaped (yellow) areas will have different number of areas in m 2 and will be used for farming, as depicted above.
What is the original green area in m 2 ?
The answer is 120.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
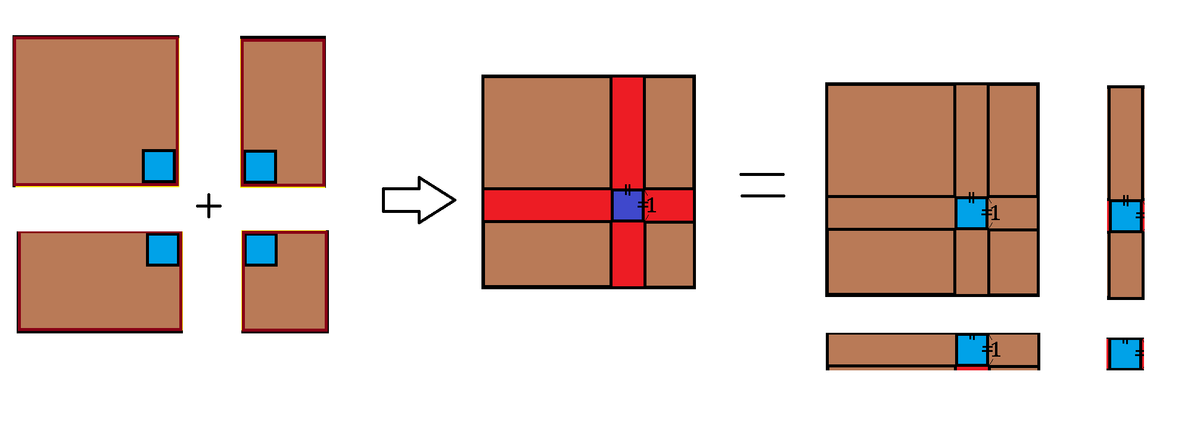
If we take the four brown rectangles to overlap within the original square, then the red rectangles will be overlapped twice while the inside deep blue square will be overlapped four times. If the side length is x , the area above will equal to x 2 + 2 x + 1 .
Then we will obtain the equation:
( x 2 − 6 3 ) + ( x 2 − 9 3 ) + ( x 2 − 8 1 ) + ( x 2 − 1 0 1 ) = x 2 + 2 x + 1
3 x 2 − 2 x − 3 4 1 = 0
( 3 x + 3 1 ) ( x − 1 1 ) = 0
Thus, x = 1 1 , and the green area = 1 1 2 − 1 = 1 2 0 .
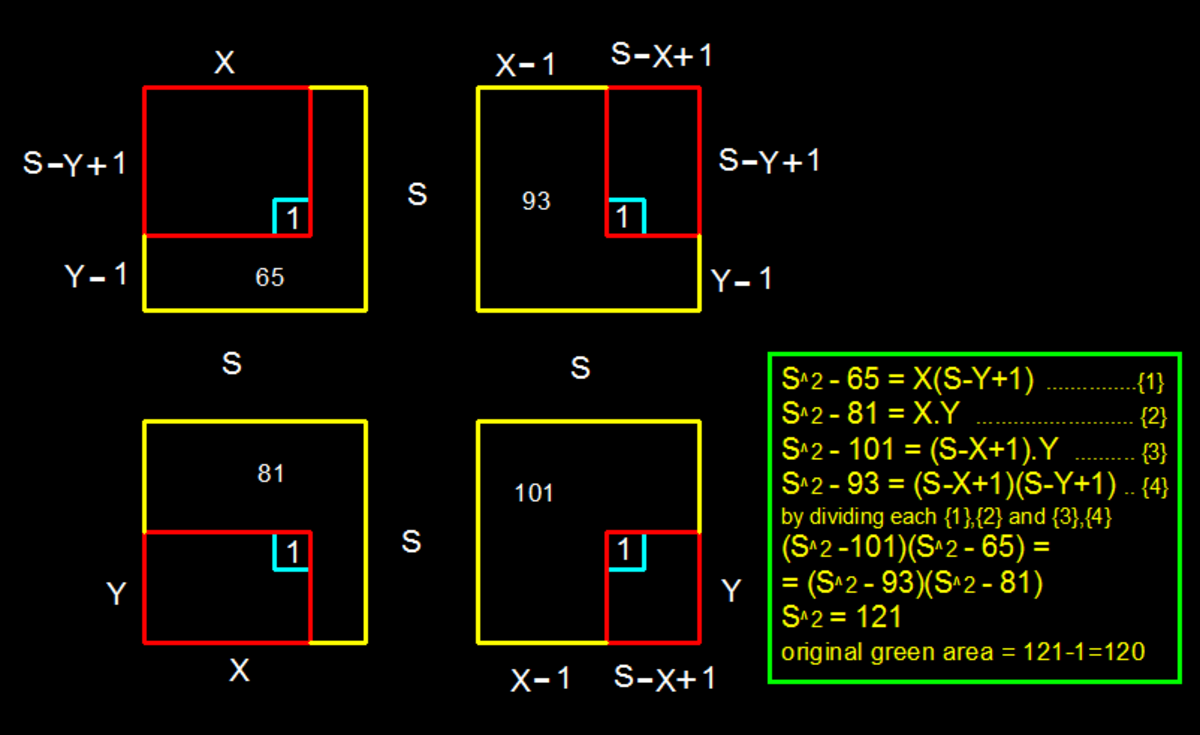
If you add all the yellow areas in the original problem together, you will have every orange part of the image above three times, every yellow part two times, and the blue part not at all. So if you take the side of the square as x , you can describe the coverage as
3 x 2 − x − x − 1 = 6 5 + 9 3 + 8 1 + 1 0 1 = 3 4 0
This equation has two solutions: x = 1 1 , x = − 3 3 1
Only the first is applicable, and the green area is 1 1 2 − 1 = 1 2 0
A solution with x = 1 1 actually exists and it is pictured below.