The easiest hardest geometry question
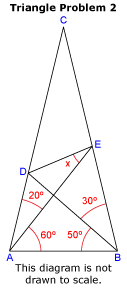 Solve for x.
This is the world's hardest and easiest Geometry question. Note that Trigonometry is NOT needed. No in depth thinking needed. Good luck, you need it.
Solve for x.
This is the world's hardest and easiest Geometry question. Note that Trigonometry is NOT needed. No in depth thinking needed. Good luck, you need it.
The answer is 30.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
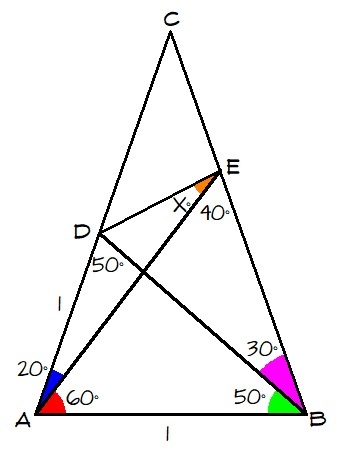 Consider the diagram.
Consider the diagram.
∠ B D A = 1 8 0 − 2 0 − 6 0 − 5 0 = 5 0
∠ A E B = 1 8 0 − 6 0 − 3 0 − 5 0 = 4 0
Since ∠ A D B = ∠ D B A = 5 0 , △ A D B is isosceles with A D = A B .
Let A D = A B = 1 .
Apply sine law on △ A E B .
sin 8 0 A E = sin 4 0 1 ⟹ A E ≈ 1 . 5 3 2
Appy cosine law on △ A D E .
( D E ) 2 = 1 2 + 1 . 5 3 2 2 − 2 ( 1 ) ( 1 . 5 3 2 ) ( cos 2 0 ) ⟹ D E ≈ 0 . 6 8 4
Apply sine law on △ A D E .
1 sin x = 0 . 6 8 4 sin 2 0
x = sin − 1 0 . 5 = 3 0 ∘
We don't have to use trigonometry.
Draw the figure and measure the angle. :P
Calculate some known angles: ACB = 180-(10+70)-(60+20) = 20° AEB = 180-60-(50+30) = 40°
Draw a line from point E parallel to AB, labeling the intersection with AC as a new point F and conclude: FCE ACB CEF = CBA = 50+30 = 80° FEB = 180-80 = 100° AEF = 100-40 = 60° CFE = CAB = 60+20 = 80° EFA = 180-80 = 100°
Draw a line FB labeling the intersection with AE as a new point G and conclude: AFE BEF AFB = BEA = 40° BFE = AEF = 60° FGE = 180-60-60 = 60° = AGB. ABG = 180-60-60 = 60°
Draw a line DG. Since AD=AB (leg of isosceles) and AG=AB (leg of equilateral), conclude: AD = AG. DAG is isosceles ADG = AGD = (180-20)/2 = 80° Since DGF = 180-80-60 = 40°, conclude: FDG (with two 40° angles) is isosceles, so DF = DG With EF = EG (legs of equilateral) and DE = DE (same line segment) conclude: DEF DEG by side-side-side rule DEF = DEG = x FEG = 60 = x+x
Answer: x = 30°