Two Wrongs Make A Right?
Nihar and Andrew are trying to find the area of △ A B C using the formula
2 1 × base × height .
Nihar mistakenly multiplies base A B by the height from A ( instead of C ) . He gets a value of 14.
Andrew mistakenly multiplies base B C by the height from C ( instead of A ) . He gets a value of 56.
Find the actual area of triangle △ A B C .
The answer is 28.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Moderator note:
Good observation about the product of these values.
Does there exist a triangle that satisfies these conditions?
Does there exist a triangle that satisfies these conditions?
I think it should be 56
Let a = A B and b be the altitude from A . Let c = B C and d be the altitude from C . We know that a b = 1 4 ∗ 2 = 2 8 and c d = 5 6 ∗ 2 = 1 1 2 .
Also, a d and b c are both the area of a triangle since the area is any base times the altitude to that base. Thus, a d = b c . If we multiply a b and c d , we get a b c d = 2 8 ∗ 1 1 2 = 3 1 3 6 . We can rearrange the expression into a d b c = 3 1 3 6 because multiplication is commutative. Since a d = b c , ( a d ) 2 = 3 1 3 6 so a d = 5 6 . Since a d is the base times the height, and you have to divide the product by 2 to get the area, a d ∗ 0 . 5 = 5 6 ∗ 0 . 5 = 2 8 which is the final answer.
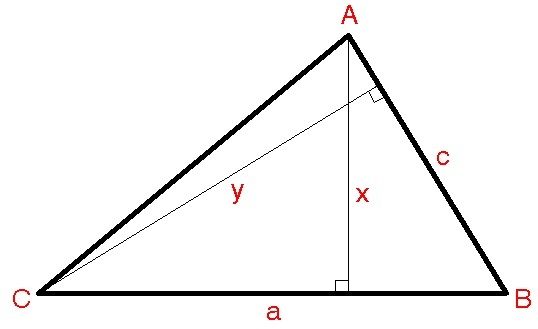
-
2 1 c x = 1 4 ⟹ c x = 2 8 ⟹ c = x 2 8
-
2 1 a y = 5 6 ⟹ a y = 1 1 2 ⟹ a = y 1 1 2
The true area must be A = 2 1 c y or A = 2 1 a x .
Since the two areas are equal,
A = A
2 1 c y = 2 1 a x
c y = a x
However, c = x 2 8 and a = y 1 1 2
We substitute
x 2 8 ( y ) = y 1 1 2 ( x )
2 8 y 2 = 1 1 2 x 2
y 2 = 4 x 2
y = 2 x
We substitute y = 2 x in A = 2 1 c y , we have
A = 2 1 ( c ) ( 2 x ) = c x = 2 8 answer

Let h 1 be the height from A . Nihar's equation gives
2 ( A B ) h 1 = 1 4
Let h 2 be the height from C . Andrew's equation gives
2 ( B C ) h 2 = 5 6
Let K be the area of △ A B C .
Both equation contain valuable information but the information is not directly useful to us. If we knew A B and h 2 or B C and h 1 , we can find K . Only way for us to get any information is by combining the two equations.
2 ( A B ) h 1 × 2 ( B C ) h 2 = 1 4 × 5 6
On rearranging,
2 ( A B ) h 2 × 2 ( B C ) h 1 = 7 8 4 K 2 = 7 8 4 K = 2 8