Only for Geometry diehards

Since the sides of triangle ACB are given to be 12, 9 and 15, it can be deduced that triangle ACB is a right angle triangle since 12, 9 and 15 form a Pythagorean triplet.

ϕ= arcsin(12/15).

2θ+ϕ= 180°.

So θ= [(180-ϕ)/2]° = [(180-arcsin(12/15)/2]° = arctan(2).

So CQ/9= 2, implying that CQ= 18.

Thus, CQ+BQ= 18+(18+12)= 48.

Let $X$ be on $BA$ produced such that $AC = AX$ and connect $XQ$ . We are given that $AC=9$ , $BC=12$ and $AB=15$ . By Pythagoras' Theorem, since $9^2+12^2=15^2$ , $\triangle ABC$ is a right-angled triangle with $\angle ACB = 90^{\circ}$ . Now, since it is given that $AQ$ bisects $\angle XAC$ , let $\angle CAQ = \angle XAQ = x$ . Then $\angle BAC = 180-2x$ and $\angle ABC = 2x-90$ . Since $AC=AX$ , $\angle CAQ = \angle XAQ$ and $AQ$ is a common side, $\triangle CAQ$ is congruent to $\triangle XAQ$ , implying that $\angle AXQ = \angle ACQ = 90^{\circ}$ and $\angle CQX = 2 \times \angle AQC = 180-2x$ . We observe that $\triangle ABC$ is similar to $\triangle QBX$ , implying that $BQ:XQ$ is in the ratio $15:9$ . Since $CQ=XQ$ , $CQ=18$ and $CQ+BQ=\boxed{48}$ .

The figure will be somewhat like this,

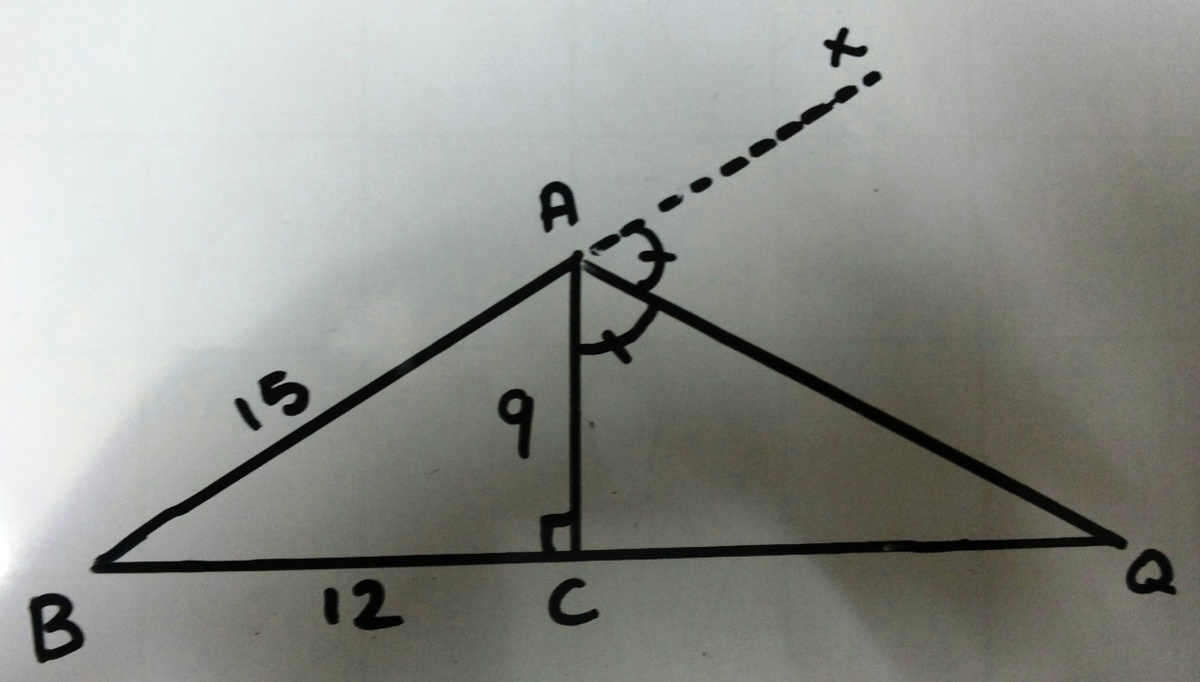
ABC is a right angeled triangle,

$\therefore \quad \quad \quad tan\left( ABC \right) =\frac { AC }{ BC } =\frac { 9 }{ 12 } =\frac { 3 }{ 4 } =0.75$

$\Longrightarrow \quad \quad \quad \angle ABC={ tan }^{ -1 }\left( 0.75 \right) =36.8699$

Now, by exterior angle property,

$\angle XAC=\angle ABC+\angle ACB=36.8699+90=\quad 126.8699$

$\Rightarrow \quad \quad \quad \quad \angle CAQ=\frac { 1 }{ 2 } \angle XAC=\quad 63.4349$

Again, triangle ACQ is a right angled triangle,

$\therefore \quad \quad \quad \quad tan\left( CAQ \right) =tan\left( 63.4349 \right) =\frac { CQ }{ AC } =\frac { CQ }{ 9 }$

$\Longrightarrow \quad \quad \quad \quad CQ=2\times 9=\quad 18$

$\therefore \quad \quad \quad \quad \quad CQ+BQ=18+18+12\quad =\quad \boxed{48}$