Only one root in common

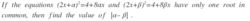
Expand both equations to get : $4x^{2} - 4ax + (a^{2} -4) = 0$ and $4x^{2} - 4bx + (b^{2} -4) = 0$ Using the quadratic formula the roots for each equation will be $\frac {4a +/- 8}{8}$ and $\frac {4b +/- 8}{8}$ respectively which can be simplified to $\frac {a}{2} + 1$ and $\frac{a}{2} - 1$ and $\frac {b}{2} +1$ and $\frac{b}{2} - 1$ out of these four only 2 should be equal one for each equation, if 1 and 3 are equal then 2 and 4 will also be equal, violating the condition so either 2 and 3 are equal or 1 and 4 are equal 》》 $\frac { a}{2} -1 = \frac {b}{2} + 1$ which gives $a -b = -4$ and it's absolute value is 4 equating the 2nd case also gives the same answer , so the answer is 4 :-)