Only real no.s
What is the minimum value of the expression 2 x 2 + 2 y 2 + 5 z 2 − 2 x y − 4 y z − 2 x − 4 z + 1 5 where x , y and z are all real numbers. If the answer can be expressed as b a where a and b are coprime positive integers, write the answer as a + b .
The answer is 86.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
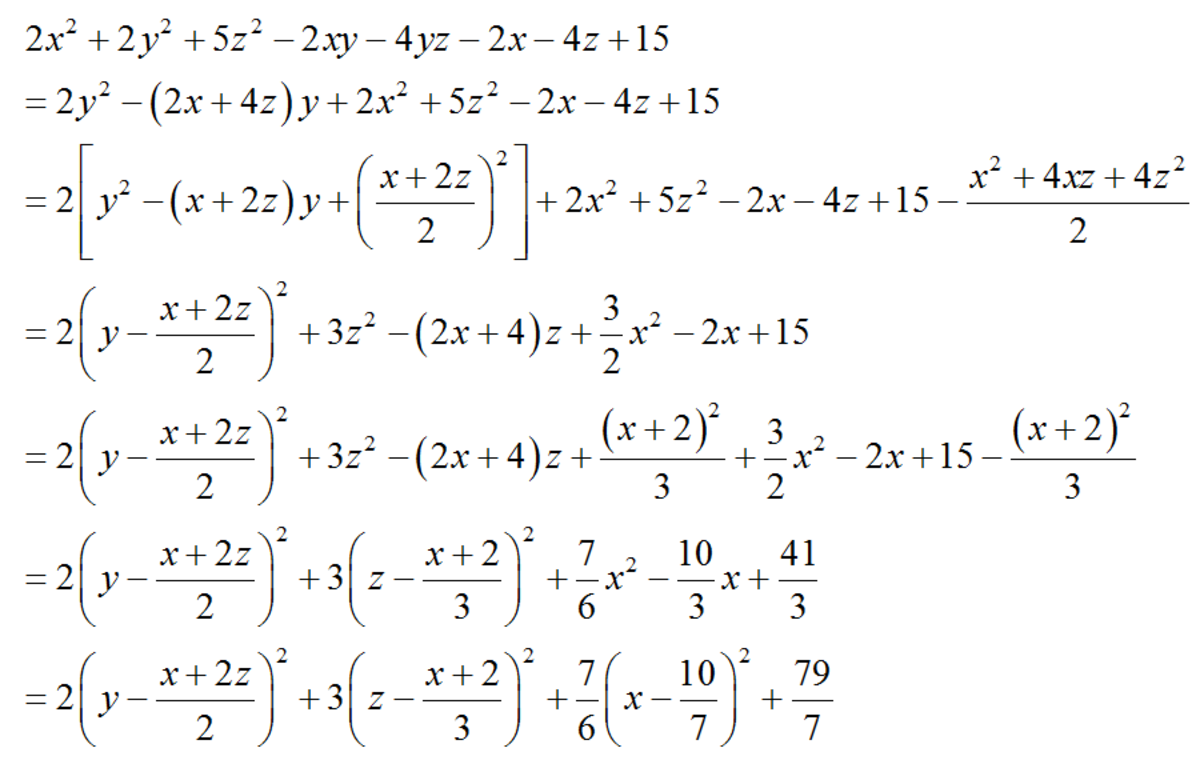
Nice solution. I wonder how much time it took you to solve this??
At the critical value (in this case it is minimum), the partial derivative with respect to x,y, and z must be 0. ∂ x ∂ f = 4 x − 2 y − 2 = 0 ∂ y ∂ f = 4 y − 2 x − 4 z = 0 ∂ z ∂ f = 1 0 z − 4 y − 4 = 0 Solving these simutaneous equations, x = 1 0 / 7 , y = 1 3 / 7 , z = 8 / 7 Substituting these values into the function, f ( x , y , z ) m i n = 7 9 / 7
Such an elegant solution, upvoted! @Potsawee Manakul