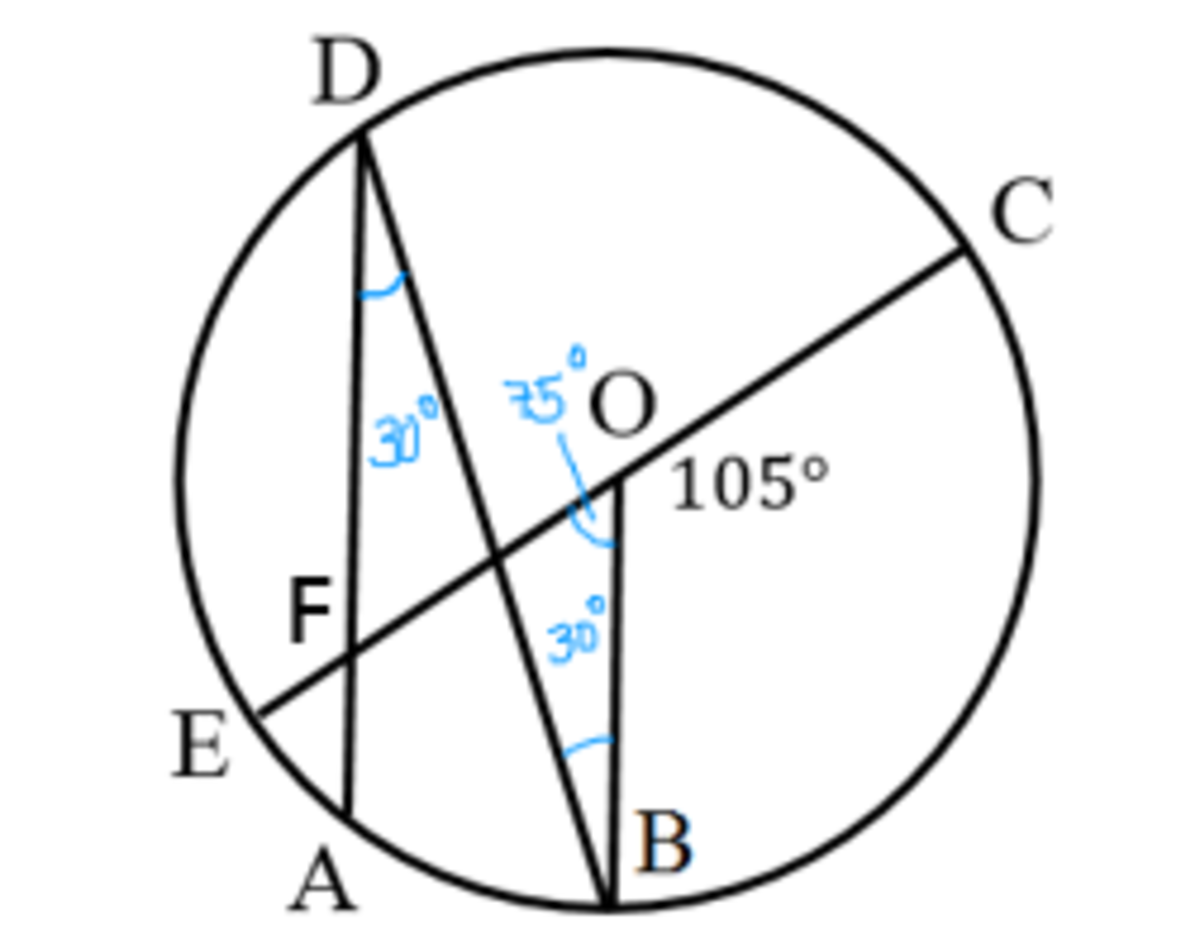
Oops! Someone Gave Out A Clue
A teacher wanted to test everyone's geometric proofing skills. Apparently, while the teacher was away, Elf bravely brought out a protractor and measured one of the angles of the circle drawn in the blackboard as shown below.
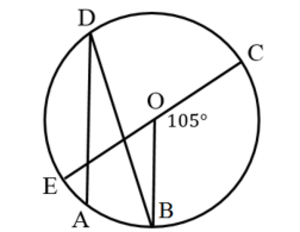
He wanted to measure but the teacher went back into the room swiftly. He got back to his seat and he was not caught but he felt uncontended.
It's time for you to solve this problem. What could be the measure of that angle?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Let's make up a proof.
PROOF 1 (My approach)
FIRST , ∠ B O C is a supplement of ∠ B O E . We know that supplementary angles have their measurements total up to 1 8 0 ∘ . Furthermore, alone, ∠ E O C measures 1 8 0 ∘ . Therefore, m ∠ B O C + m ∠ B O E = 1 8 0 ∘ .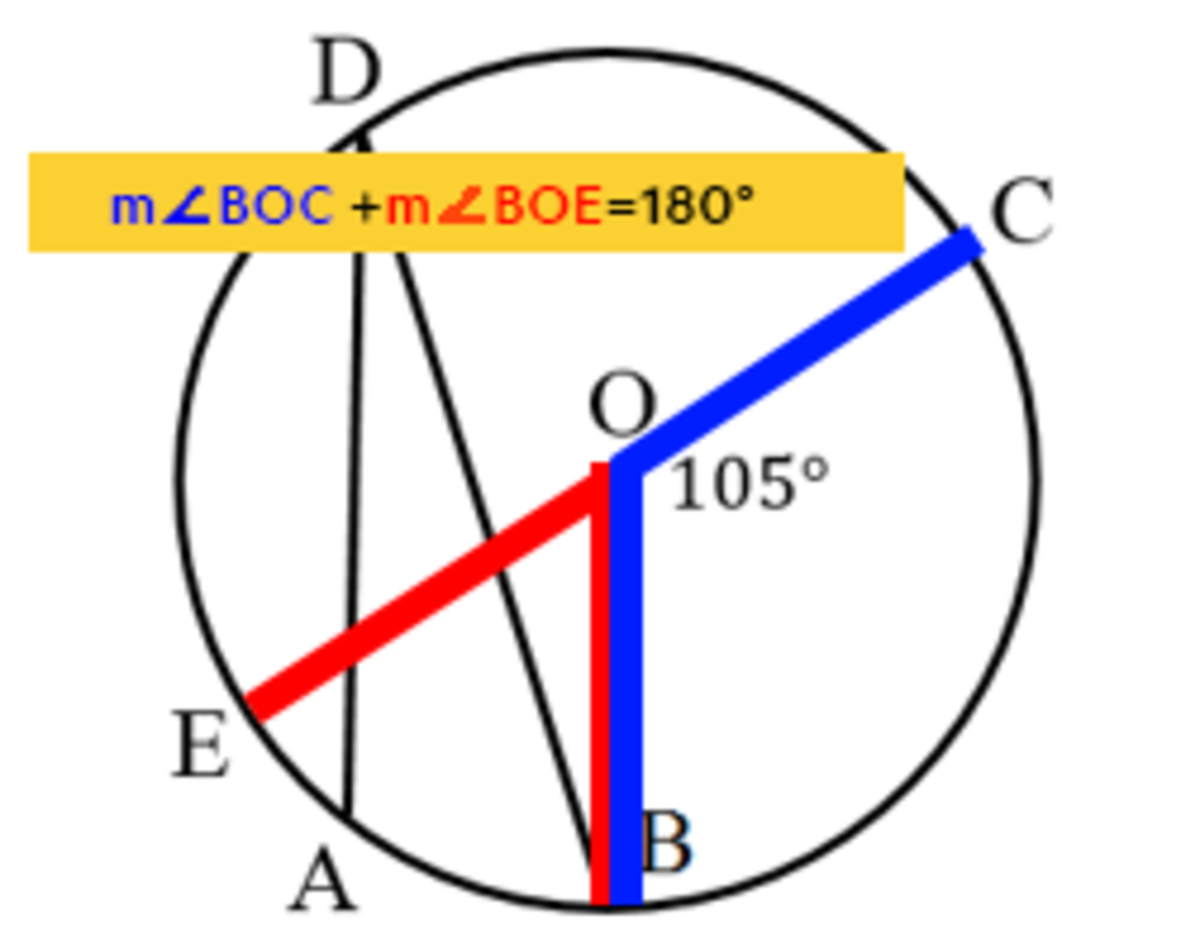 Since
m
∠
B
O
C
=
1
0
5
∘
, then we should subtract it from
1
8
0
∘
:
1
8
0
∘
−
1
0
5
∘
=
7
5
∘
⇒
m
∠
B
O
E
Since
m
∠
B
O
C
=
1
0
5
∘
, then we should subtract it from
1
8
0
∘
:
1
8
0
∘
−
1
0
5
∘
=
7
5
∘
⇒
m
∠
B
O
E
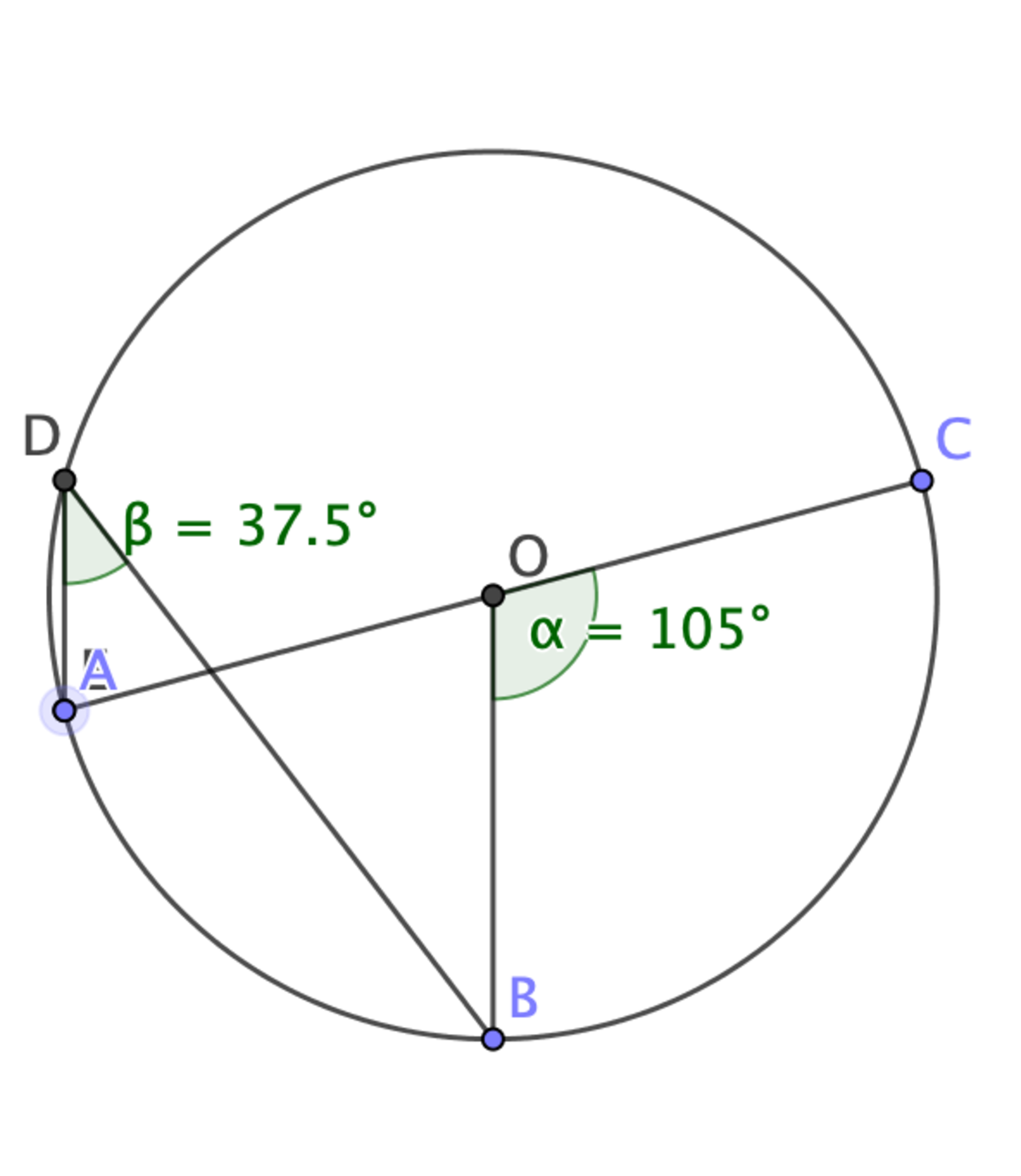
SECOND , line A D ∥ line B O .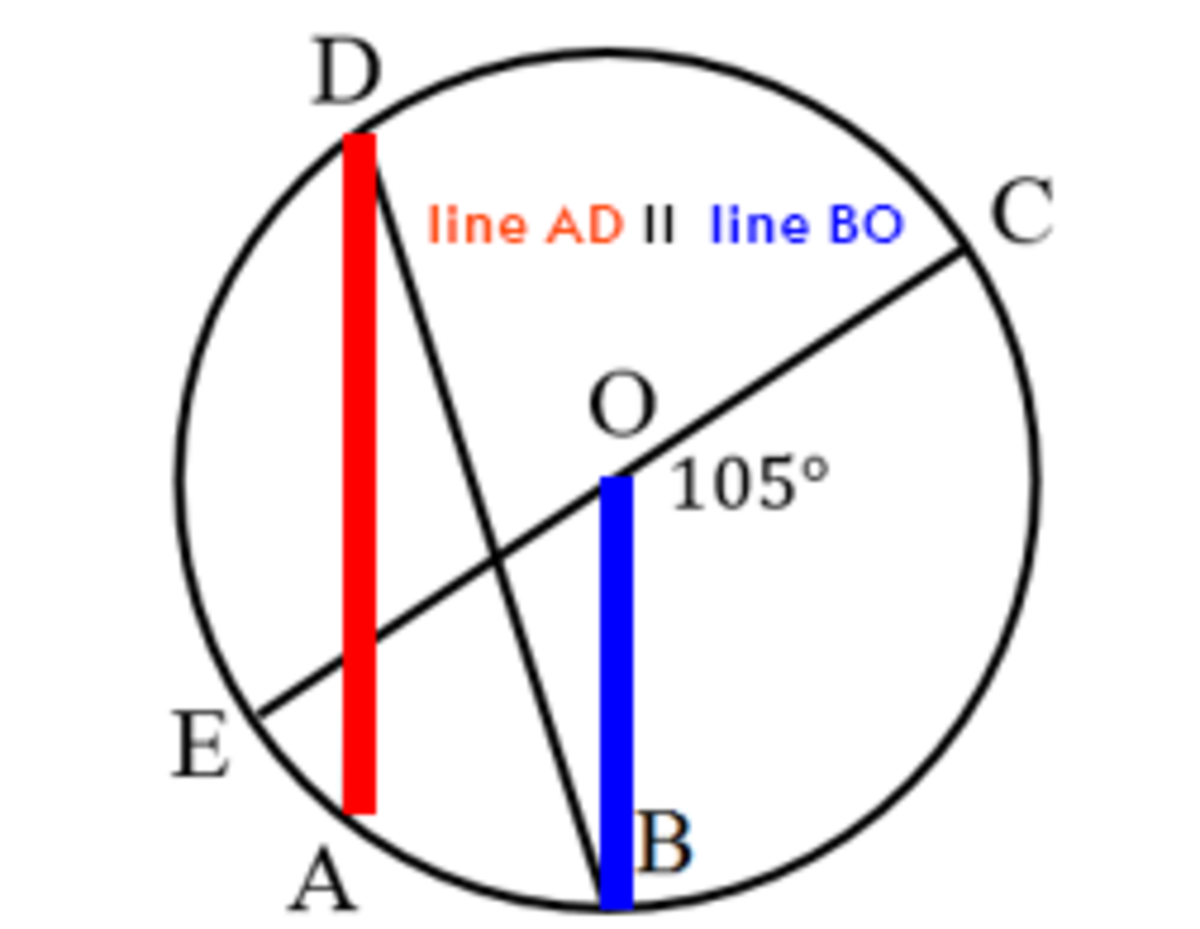 Since line
A
D
∥
line
B
O
, then we can also conclude that
m
∠
A
F
E
=
m
∠
B
O
E
=
7
5
∘
and
m
∠
A
F
C
=
m
∠
B
O
C
=
1
0
5
∘
, as shown in the images below:
Since line
A
D
∥
line
B
O
, then we can also conclude that
m
∠
A
F
E
=
m
∠
B
O
E
=
7
5
∘
and
m
∠
A
F
C
=
m
∠
B
O
C
=
1
0
5
∘
, as shown in the images below:
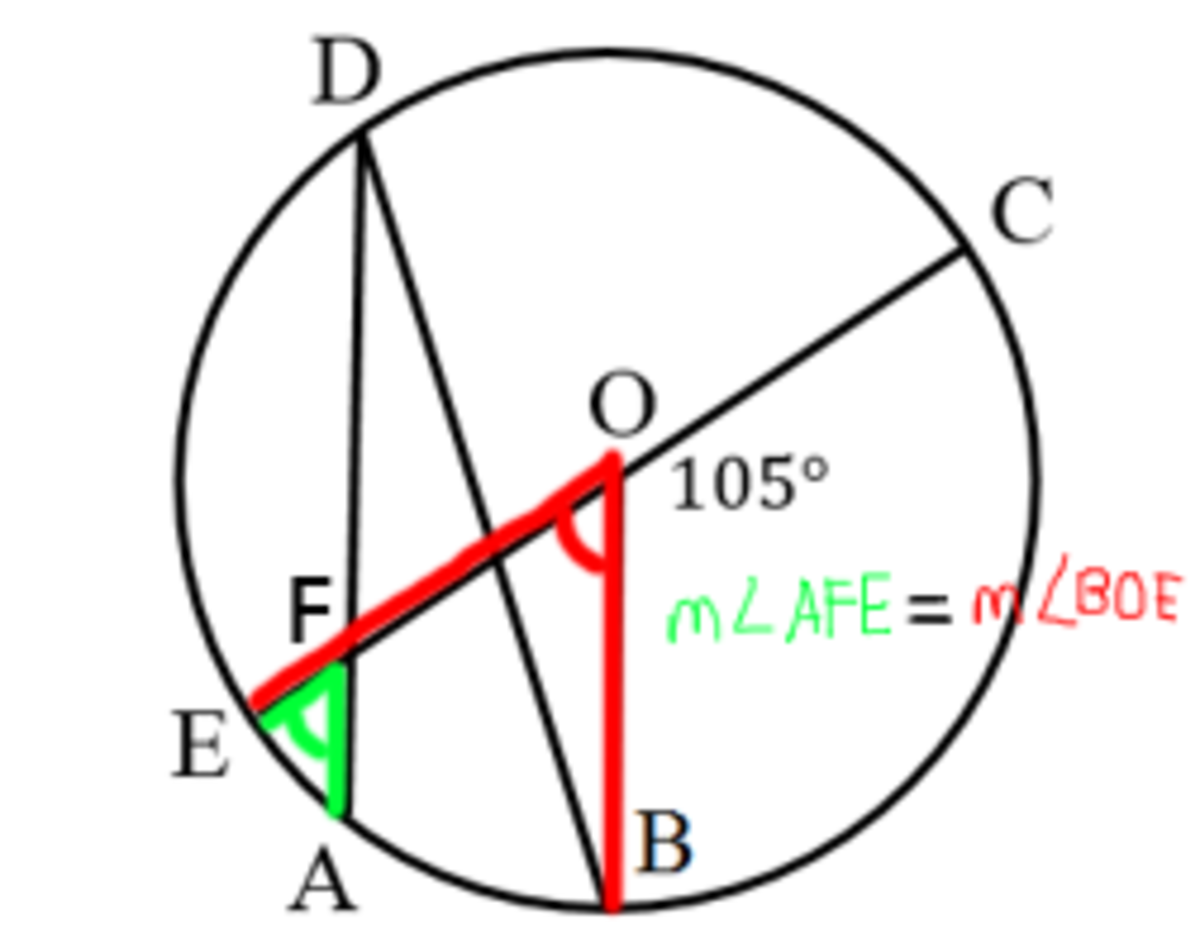
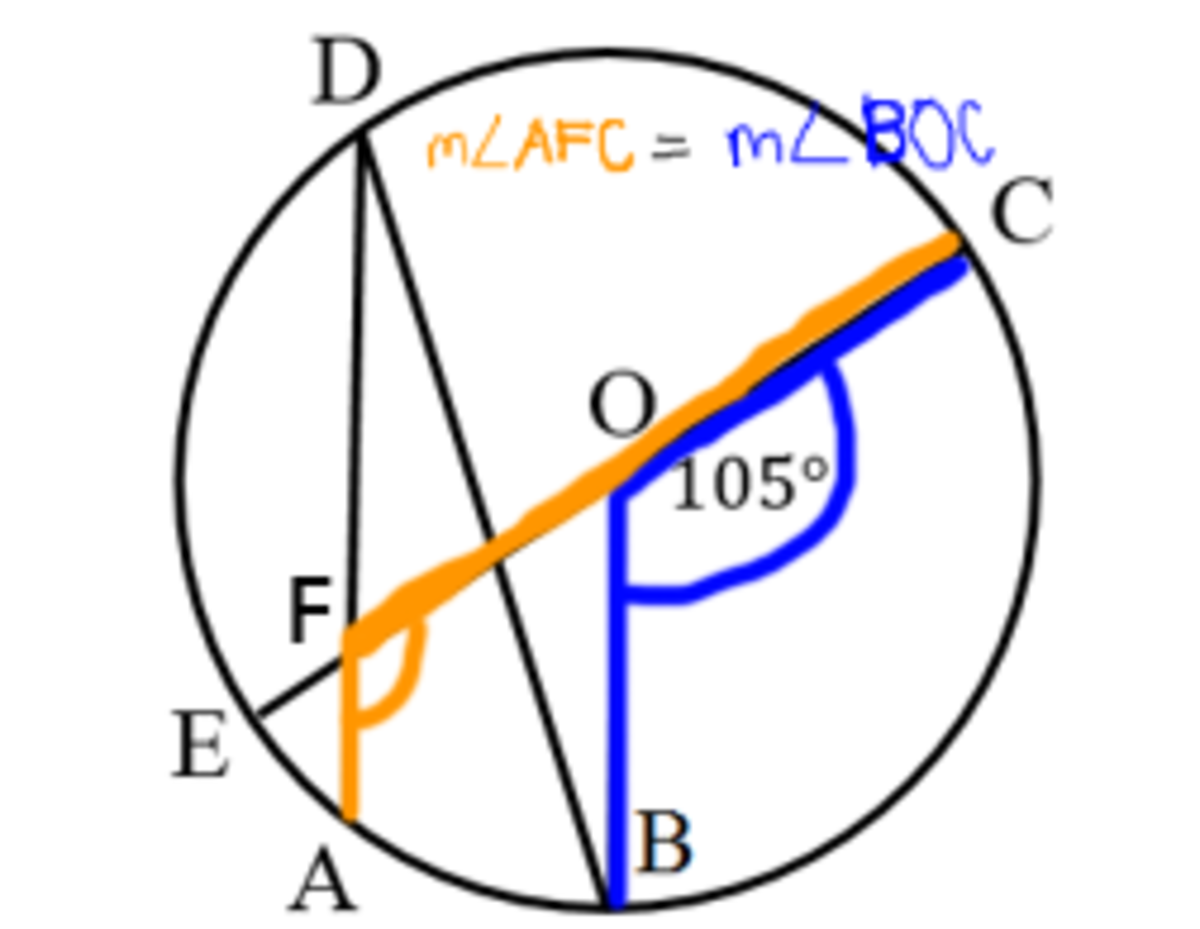
THIRD , extend line A D beyond the circle. After that, draw a tangent line that is parallel to line E C . We call this tangent line as line X Y .
Notice that the measurements depicted in the section of line E C equals the measurements formed on the section of line X Y . Then, by the application of the fact that "opposite angles have the same measurements," we can now find the m ∠ A D B .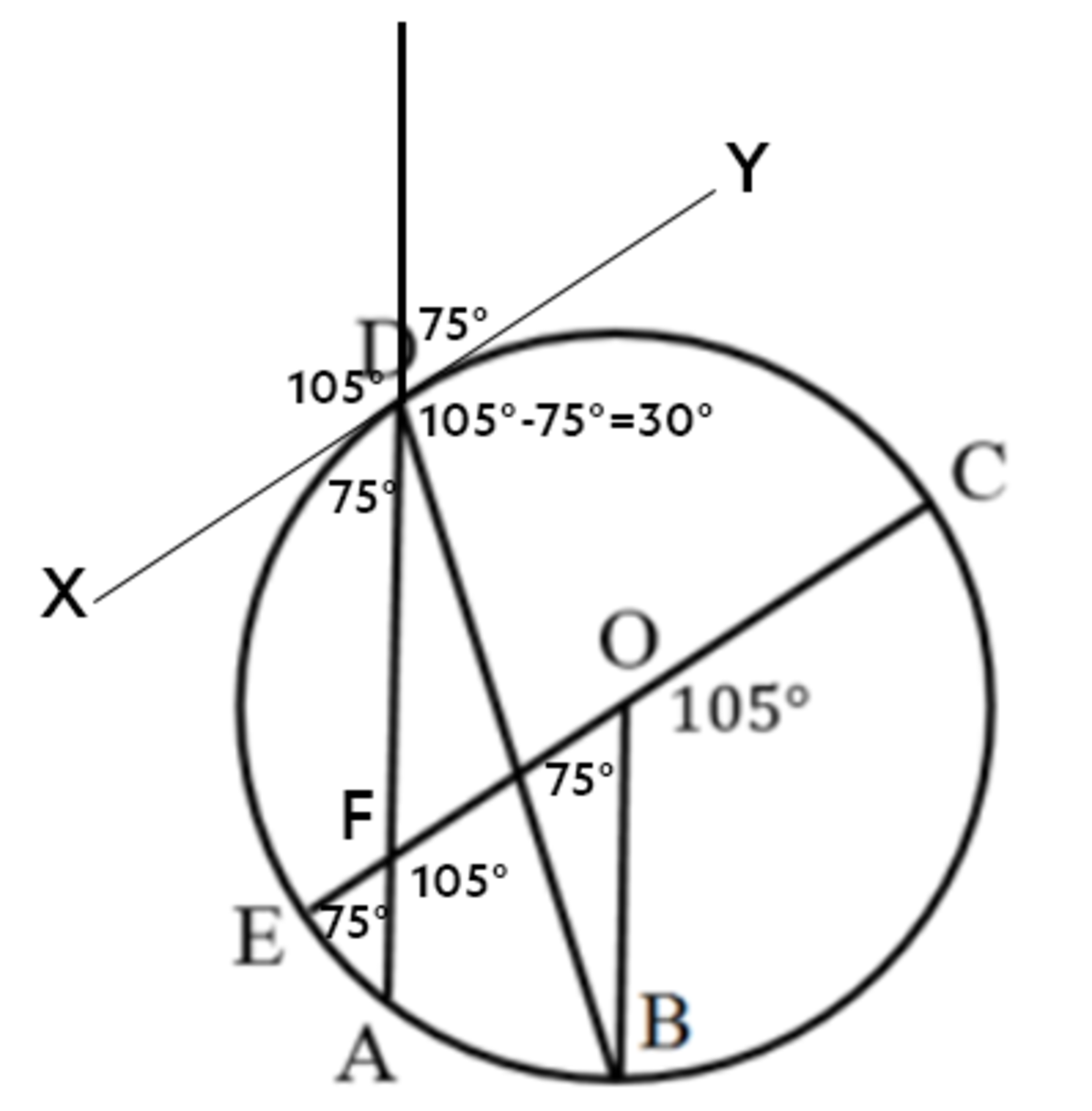 .
.
Hence, the answer is 3 0 ∘ .
PROOF 2
Another way to settle up a proof is by using the exterior angle property of triangles .
∠ E O B = 1 8 0 ∘ − 1 0 5 ∘ = 7 5 ∘ (linear pair).
Then, ∠ D B O = 1 0 5 ∘ − 7 5 ∘ = 3 0 ∘ (By exterior property of triangles).
*Note: ∠ A D B and ∠ D B O are co-interior angles.