Op Amp Filter Transient
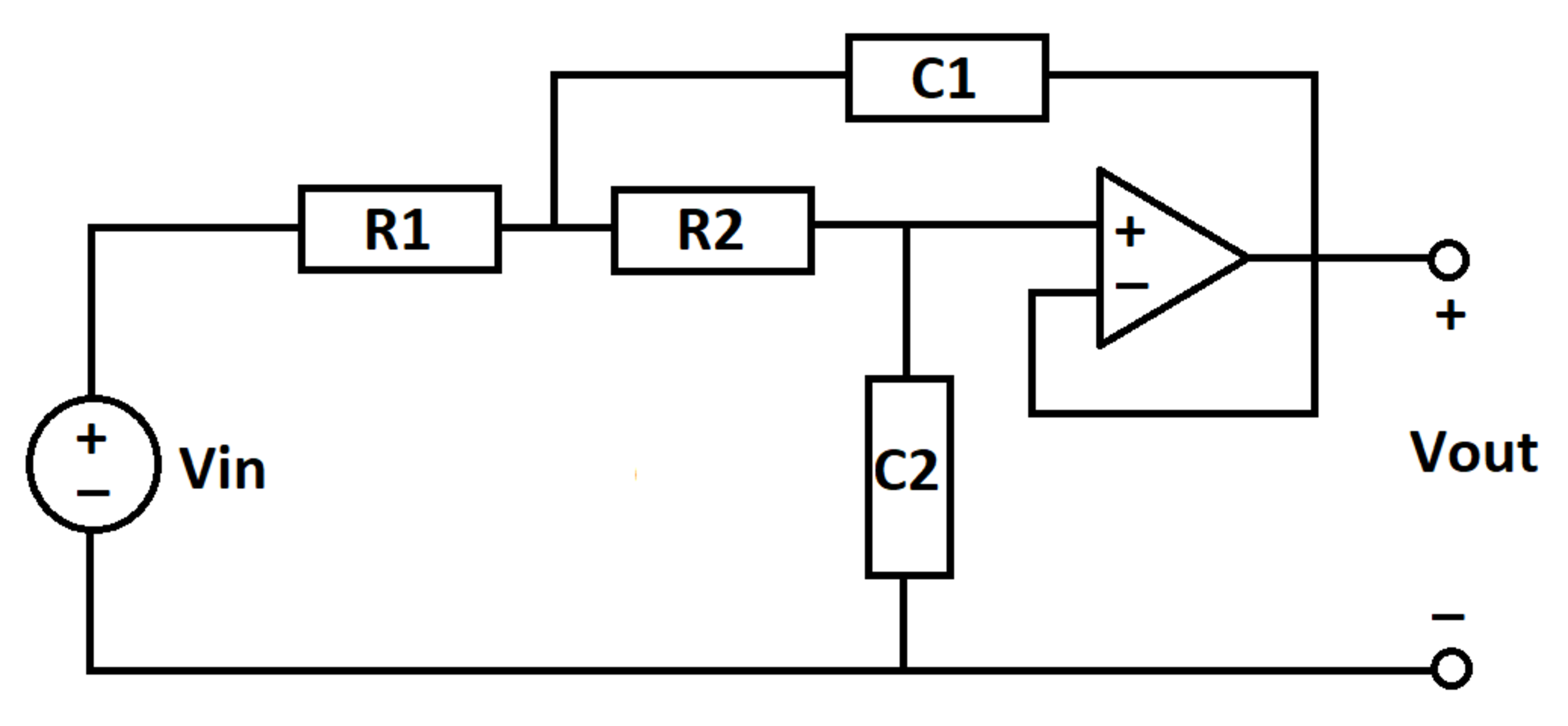
A low-pass filter is built around an ideal operational amplifier. At time t = 0 , the capacitors are de-energized. The input voltage V i n ( t ) = 1 + cos ( 3 t ) . Determine the following integral:
∫ 0 2 0 ∣ 1 − V o u t ( t ) ∣ d t
Details and Assumptions:
1)
R
1
=
R
2
=
C
1
=
C
2
=
1
2)
The voltages at the
+
and
−
terminals of the op amp are the same
3)
The currents into the
+
and
−
terminals of the op amp are zero
Bonus: Comment on the output voltage in relation to the input voltage, and how that corresponds to the nature of the filter
The answer is 2.933.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you very much for posting this problem. I got a chance to learn and test something new to me
Log in to reply
Glad you liked it. I had pretty much exhausted all of the RLC transient circuits I could think of, so I added a new element.
Log in to reply
Thanks for sharing your solution. This RLC problem set has been fun. I would gladly give any new variants of this problem a shot.
@Karan Chatrath has provided a nice explanation already. I will show my approach as well, since there are some minor stylistic differences. I also want to point out that the filter obeys the principle of superposition. Since it is a low-pass filter, the DC component passes through without attenutation, while the AC portion is greatly reduced. As it turns out, the frequency of the AC portion is three times the cutoff frequency of this filter. This is known as a Sallen-Key topology.
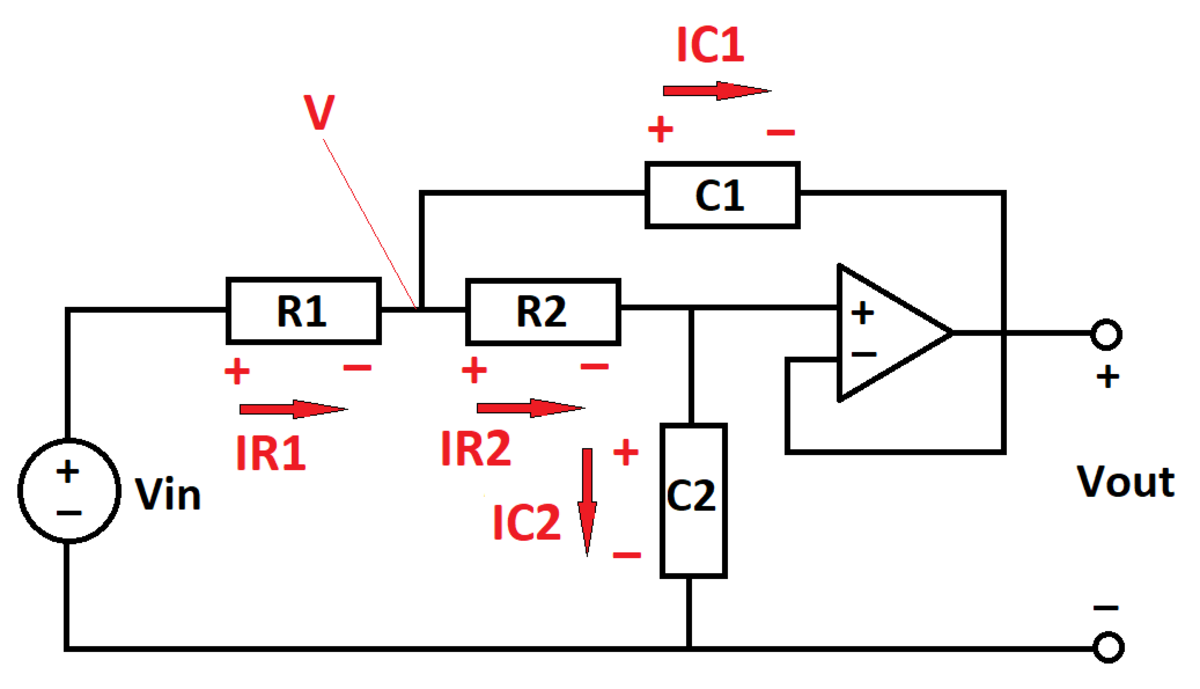
The state-space model is:
V = V C 2 + V C 1 ∗ I R 2 = R 2 V − V C 2 I R 1 = R 1 V i n − V I C 2 = I R 2 ∗ ∗ I C 1 = I R 1 − I R 2 I C 1 = C 1 V ˙ C 1 I C 2 = C 2 V ˙ C 2 ∗ from op amp voltage property ∗ ∗ from op amp current property
Consider the diagram as labelled above. The currents and junctions have been assigned a name.
Let the voltages at junctions P , Q , R , S and T respectively be V P , V Q , V R , V S , V T = 0 . The charges on the capacitors C 1 and C 2 are Q 1 and Q 2 respectively. Therefore:
I 1 = Q ˙ 1 I 2 = Q ˙ 2
As per the circuit diagram above, the following equations can be generated.
− V i n + I R 1 + I 2 R 2 + C 2 Q 2 = 0 V i n − V P = I R 1 V P − V R = C 1 Q 1 V Q − V T = C 2 Q 2 ⟹ V Q − 0 = C 2 Q 2
Considering an ideal operational amplifier, I have had no prior experience of working with them, so I had to read up a bit. What I understood was that the input current I i n = 0 for the ideal case and that V Q = V S .
Using these bits of information gives us the following equations:
V R = V S = V o u t = V Q ⟹ V Q = V o u t = C 2 Q 2
Moreover, Kirchoff's current law dictates that:
I = I 1 + I 2
Manipulating, rearranging and simplifying the above equations leads to the following system of equations:
− V i n + I + I 2 + Q 2 = 0 − V i n − I − V o u t = Q 1 I 1 = Q ˙ 1 I 2 = Q ˙ 2 I = I 1 + I 2 V o u t = Q 2
The above system of equations can be recast into a state-space form and is solved numerically to obtain the output voltage as a function of the input voltage. The required integral is also computed numerically. The numerical details are left out and I will attach if requested. This solution lays out the outline of the problem-solving approach.
The answer is:
∫ 0 2 0 ∣ 1 − V o u t ∣ d t ≈ 2 . 9 3 3
The plot showing input and output voltage is as follows:
It can be seen that the transients die out somewhere between five and six seconds after start of the simulation, and the amplitude of the steady-state output is highly attenuated. I suppose there might be some kind of electronic application where such a filter proves to be useful. Would like to know more.