Open Box Volume

After cutting a square in each corner of the metallic sheet, the dimension of the box is $32 \times 20 \times 8$ .

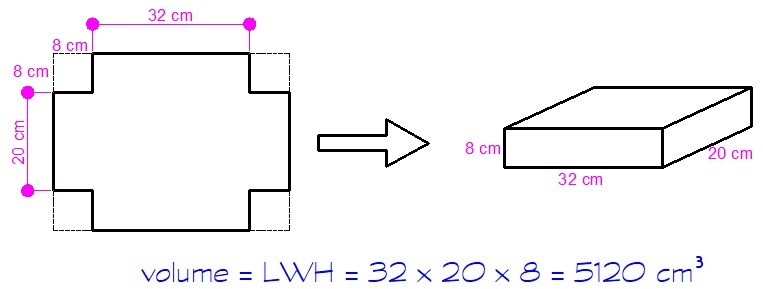
The volume of a rectangular prism is given by the formula: $V=L \times W \times H$ where $L=length, W=width$ and $H=height$ .

Substituting, we get $V=32 \times 20 \times 8 =$ $\color{#D61F06}\large \boxed{ 5120~cm^3}$

In cutting the corners of the 48cm by 36cm rectangle, the length and width are reduced to 48 - 16 and 36 - 16 respectively. Now we have that the length is 32cm and the width is 20cm. The flaps that have now been created can be folded up to make a box with a height of 8cm. The volume of this box will then be $32 \times 20 \times 8 = 5120$ cm $^3$ .

$\text{volume}=(48-8-8)(36-8-8)(8)=\large{\boxed{\text{5120 cubic cm.}}}$