Operational Amplifier (3)
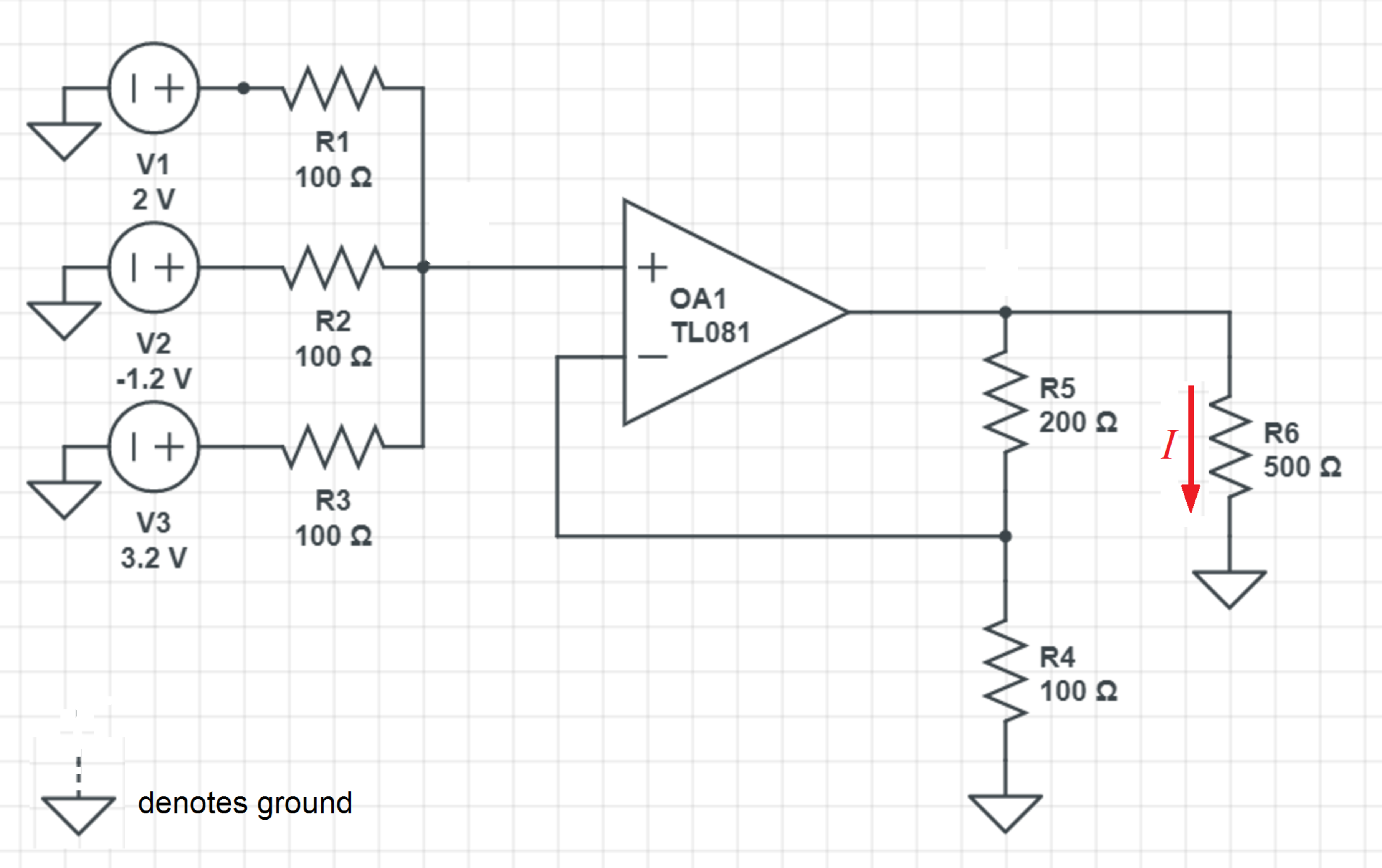
Consider the operational amplifier circuit above. Find the current I through R 6 in m A .
Hint: Try part 2 before trying this problem.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
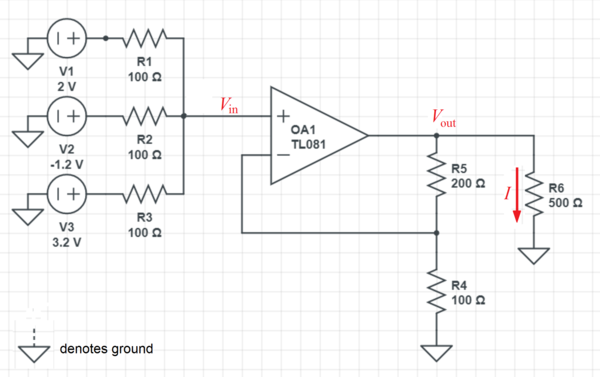
The current through R 6 is I = R 6 V o u t = 5 0 0 V o u t = 2 V o u t m A . To find V o u t , we note that the closed loop voltage gain of the non-inverting OpAmp is given by:
A V V i n V o u t V o u t = R 4 R 5 + R 4 = 1 0 0 2 0 0 + 1 0 0 = 3 V i n
To find V i n , we consider that the current flowing in the non-inverting input (marked "+") is zero. Then we have:
R 1 V 1 − V i n + R 2 V 2 − V i n + R 3 V 3 − V i n 1 0 0 2 − V i n + 1 0 0 − 1 . 2 − V i n + 1 0 0 3 . 2 − V i n 2 − 1 . 2 + 3 . 2 − 3 V i n ⟹ V i n ⟹ V o u t = 0 = 0 = 0 = 3 4 3 × 3 4 = 4 V
Therefore I = 2 V o u t = 8 m A .
From the previous problem, we know that the output voltage V = 4 . The current through R 6 is easily calculated.
I R 6 = 5 0 0 4 = 1 0 0 0 8 = 8 m A