Opposing Pentagons

The $10$ vertices of this figure are part of the $12$ vertices of a icosahedron, so we can go look that up, the dihedral angle, which is

$\pi - ArcCos \left( \dfrac { \sqrt{5} } {3} \right) = 138.19°$

This confirms your computed answer.

Suppose the top and bottom pentagons both could be inscribed in a unit circle, one pentagon is in the x-y-plane, the other one is in the plane z=h. Then one pentagon has vertices $(\cos \frac{2k\pi}{5}, \sin \frac{2k\pi}{5}, 0)$ and the other has vertices $(\cos \frac{(2k+1)\pi}{5}, \sin \frac{(2k+1)\pi)}{5}, h)$ .

First find h.

A side of a pentagon, for example between $(1,0,0)$ and $(\cos\frac{2\pi}{5}, \sin\frac{2\pi}{5}, 0)$ has squared length $(\cos\frac{2\pi}{5}-1)^2+\sin^2\frac{2\pi}{5}+0 = 2-2\cos\frac{2\pi}{5}=1.381966$ , this should be equal to the squared length of an edge connecting the pentagons, which is $2-2\cos\frac{\pi}{5}+h^2=0.381966+h^2$ , so it turns out that $h=1$ .

Now find the distance d between the tops of two adjacent triangles. The distance between $(\cos \frac{2\pi}{5}, \sin \frac{2\pi}{5}, 0)$ and $(\cos \frac{9\pi}{5}, \sin \frac{9\pi}{5}, 1)$ is $1.902113$ .

The height of a triangle is $\frac{1}{2}\sqrt{3}$ times a side of it, so $\frac{1}{2}\sqrt{3}\sqrt{ 2-2\cos\frac{2\pi}{5}} =1.0180739$

The sine of the angle $\alpha$ we are looking for is half the distance divided by the triangle height.. $\sin (\alpha/2) = 1.90213 /( 2×1.018)$ and $\alpha =2 \arcsin (0.93417) =\boxed{138.19°}$

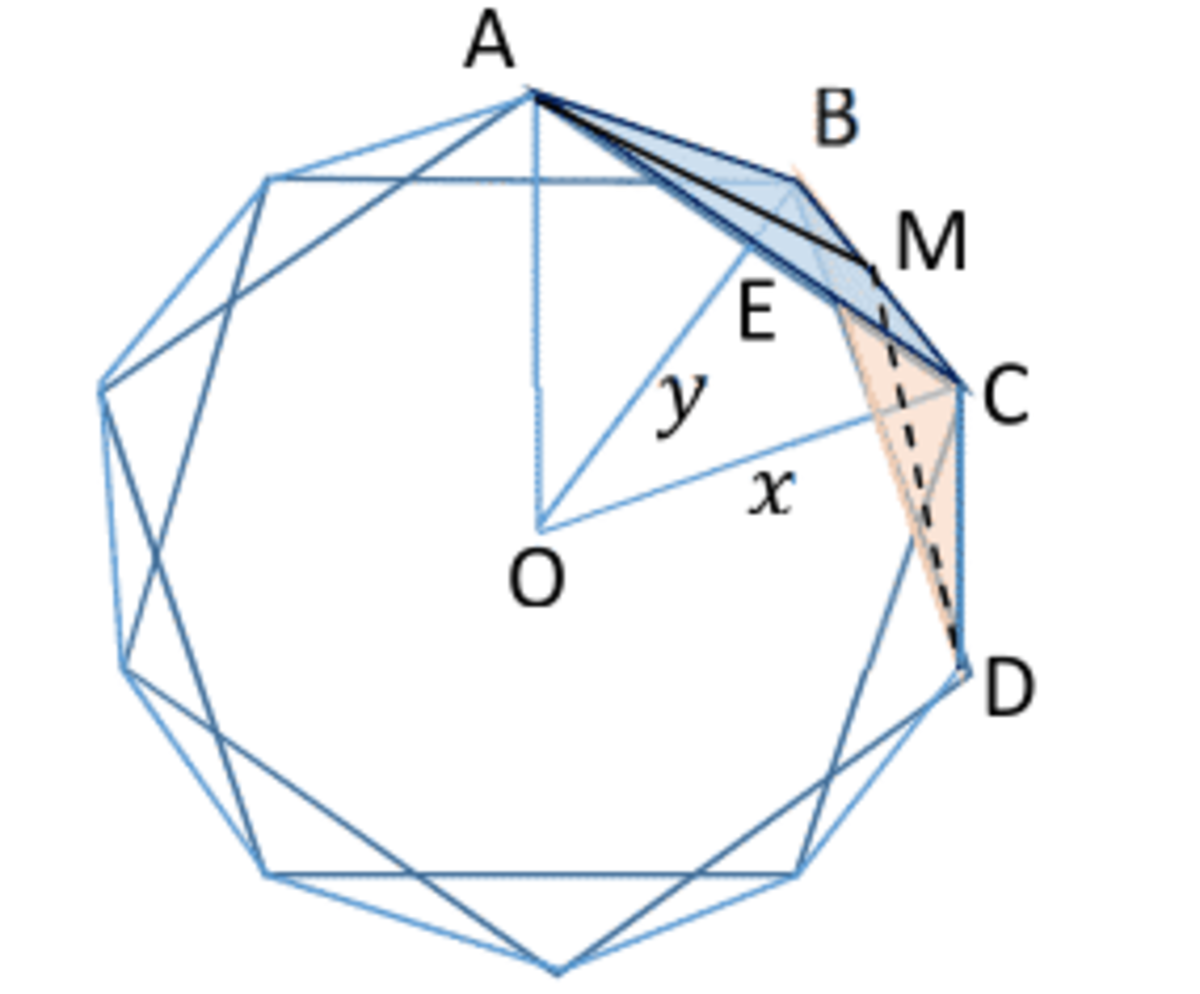
The image pictures the solid as seen from above one of the pentagonal faces. Triangle $\triangle ABC$ , foreshortened in the image, is in reality an equilateral triangle with side 1. The distance $x$ from the center of the pentagon to its vertex can be obtained from $\triangle OEC$ using the fact that $\angle EOC=36^\circ$ and $\overline{EC}=1/2$ .

$x=\frac{1}{2 sin(36^\circ)}=0.85065$

$\overline{OE}=y=x\times cos(36^\circ)=0.68819$

The foreshortened distance $\overline{EB}=x-y=0.16246$ (foreshortened due the slant of the $\triangle ABC$ ). However in reality $\overline{EB}$ is the height of an equilateral triangle side 1, that is its length is equal to $\sqrt{3}/2$ . From this we can get the perpendicular distance between the pentagons as $h=\sqrt{3/4-(x-y)^2}=0.85065$ (same distance as the $x=\overline{OC}$ interestingly enough.)

To get the angle between two adjoining triangles, we will use triangles $\triangle ABC$ and $\triangle BCD$ . The lines $\overline{AM}$ and $\overline{MD}$ are perpendicular to $\overline{BC}$ and are both equal $\sqrt{3}/2$ . If we can find the actual distance between A and D, we can use the $\triangle AMD$ to calculate the angle between the adjoining triangular faces.

Horizontal component of the distance $\overline{AD}$ (that is the one in the plane of the pentagons), can be obtained from the fact that both A and D are $x$ from O, and that $\angle EOD=72^\circ+36^\circ$ . It comes to $2\times x \times sin(54^\circ)=1.37638$ . Vertical component of the distance is the distance between the planes of the pentagons $h$ . So the actual

$\overline{AD}=\sqrt{1.37638^2+h^2}=1.618$

From $\triangle AMD$ the angle between the triangles is

$2\times arcsin(\overline{AD}/\sqrt{3})=138.19^\circ$

The solid we have been studying is known as a pentagonal antiprism. It can be obtained from an icosahedron by slicing off two opposing vertices with their associated sides, and by doing so producing the two pentagons. It’s not at all surprising therefore that the angle between the triangles is the dihedral angle of an icosahedron.