Opposite Slopes

Geometry Level 3

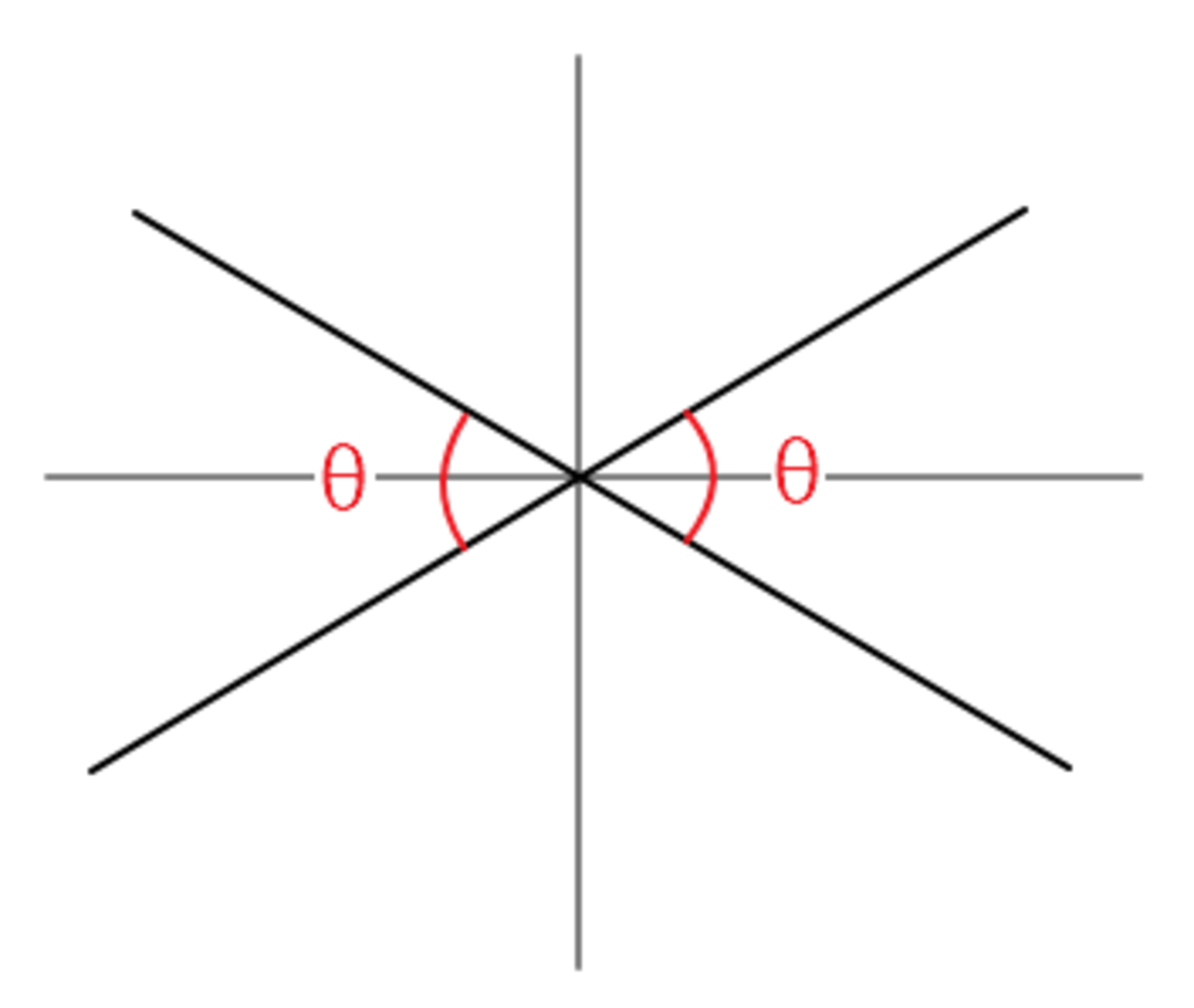Given any two lines with slopes $m_{1}$ and $m_{2}$ , where $m_{1}$ and $m_{2}$ are opposites (i.e. $m_{2} = -m_{1}$ ), which expression describes either of the two angles formed on either side of their intersection?

cos~(\frac{m_{1}}{m_{2}})

sin^{-1}~m_{1}m_{2}

\frac{m_{1}m_{2}}{2}

2~tan^{-1}~m_{1}

1 solution

David Stiff
Jul 7, 2018

We know that the slope of a line is equal to its change in $x$ over its change in $y$ , or $\dfrac{\Delta x}{\Delta y}$ .

However, if we look at half of the angle in question, namely the angle between the x-axis and one of the lines (labeled $\dfrac{\theta}{2}$ in the diagram to the right), we can see that the line's slope ( $m_{1}$ ) is actually equal to the tangent of the angle ( $tan~x = \dfrac{opposite}{adjacent} = \dfrac{\Delta x}{\Delta y} = m_{1}$ ).

Finally, since this angle is only half of the angle we want (the angle to the right or left of the intersection), our final answer must be twice the tangent of the slope, or $\boxed{2~tan^{-1}~m_{1}}$ .

Opposite Slopes

1 solution

0 pending reports