Optical Mathematics

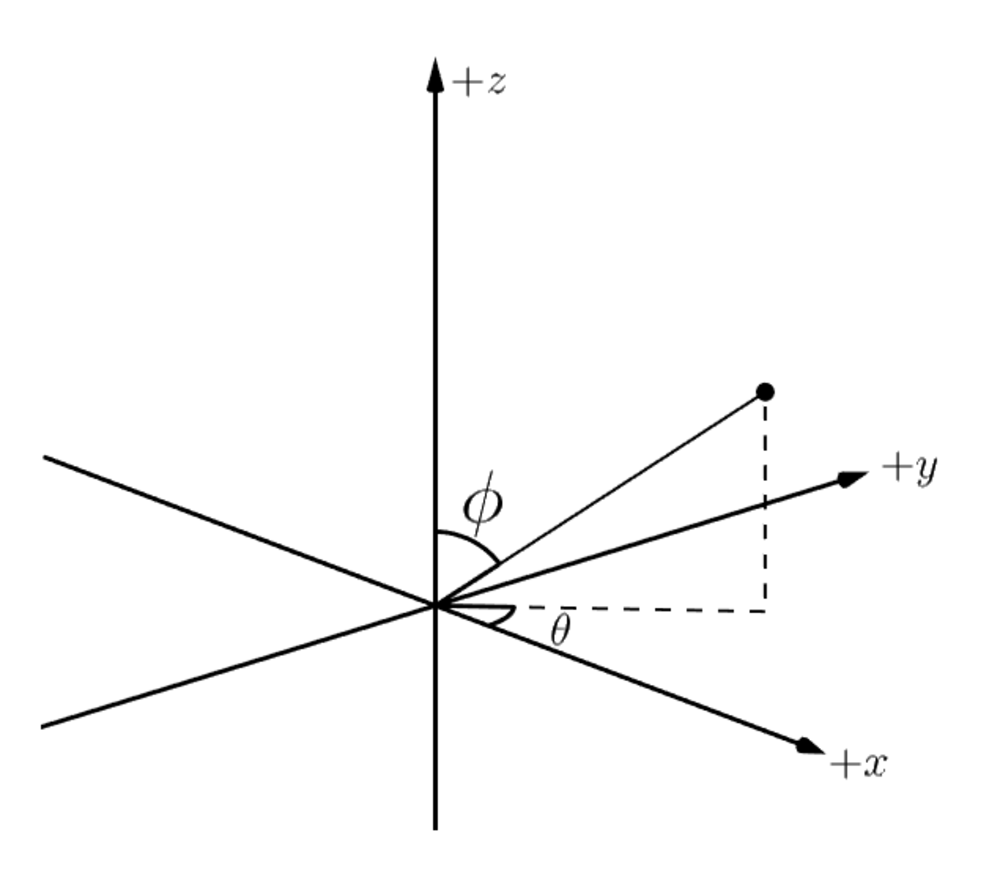
First, consider the following mapping from Cartesian coordinates to spherical coordinates:

$\begin{aligned} x &= r\cos\theta\sin\phi\\ y &= r\sin\theta\sin\phi\\ z &= r\cos\phi \end{aligned}$

where $\theta$ is the angle in the $xy$ -plane with respect to the $+x$ -axis and $\phi$ is the angle with respect to the $+z$ -axis.

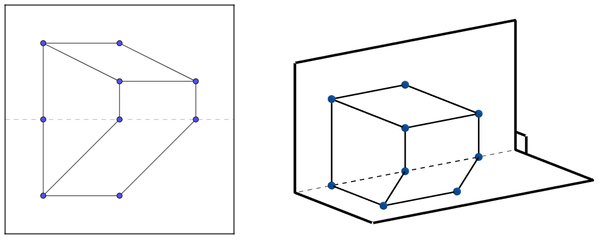
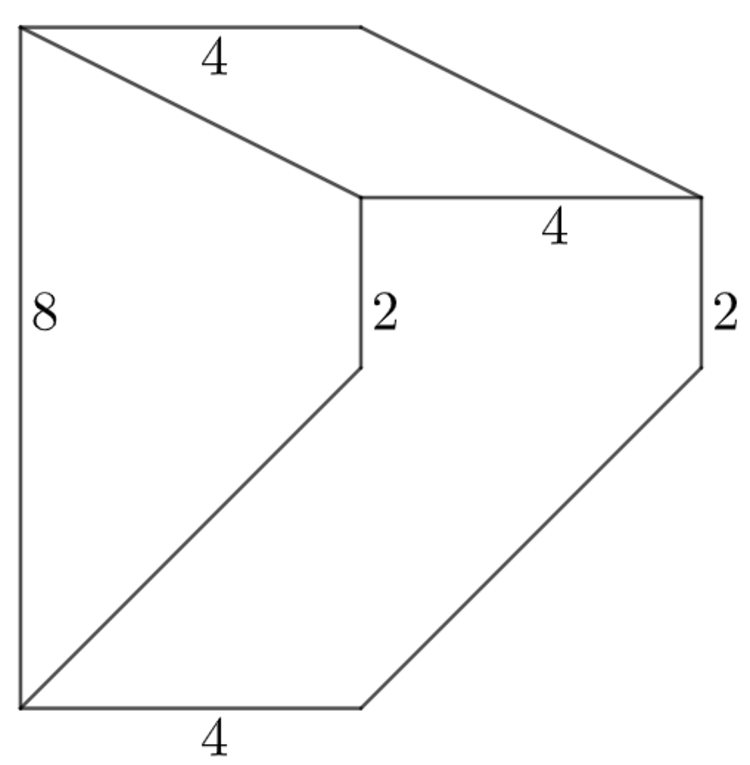
Then, construct the figure, where the dashed line passing through the points given are parallel to the horizontal segments, and also perpendicular to those three vertical segments (where the leftmost segment is bisected). The lengths of the inner figure before the fold are given on the right. If we look at the folded paper that way (above right) with one eye opened, the drawn figure appears to be a solid, where the original lengths of the segments are left unchanged. However, the figure is not visually a cube as some chosen values of $\theta$ and $\phi$ do not align the bottom portion with the top.

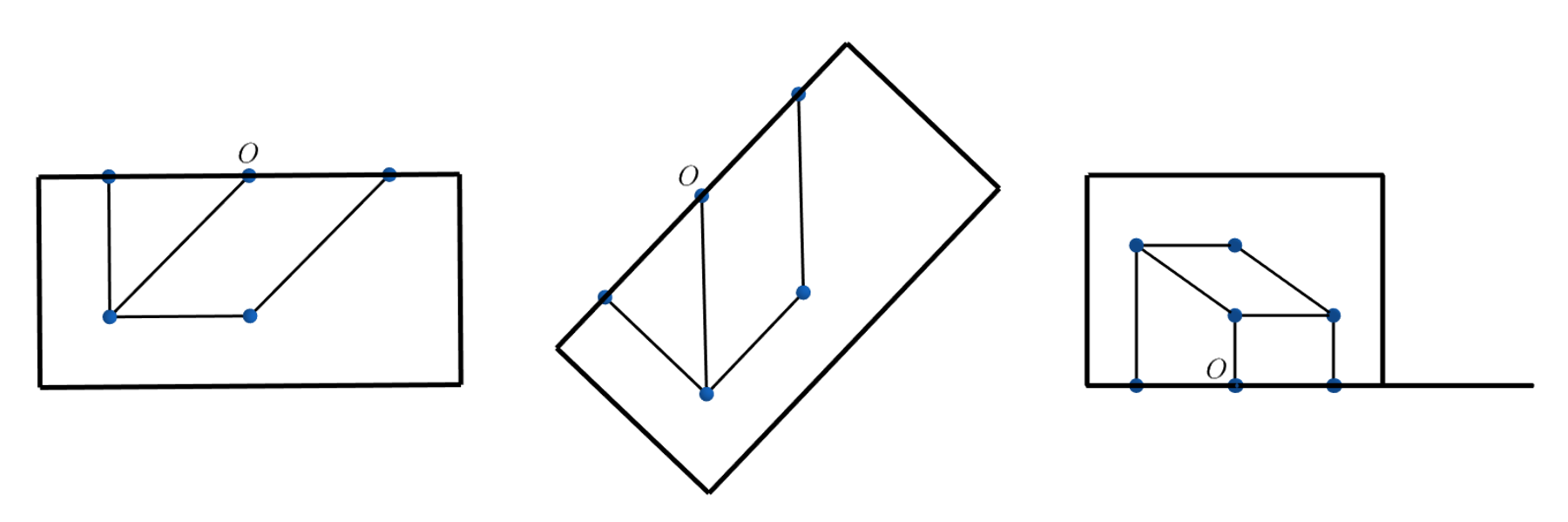
For simplicity, label the central point on the dashed line as $O$ and align the paper as shown on the left, where $\theta = 0^{\circ}$ and $\phi = 0^{\circ}$ . With respect to $O$ ,

• $\theta$ is the angle that rotates the paper counterclockwise (in the positive direction).
• $\phi$ is the angle that rotates the paper upward.

As examples, from center to right,

• $\theta = 45^{\circ}$ and $\phi = 0^{\circ}$ , showing that the paper is rotated counterclockwise at $45^{\circ}$ .
• $\theta = 45^{\circ}$ and $\phi = 90^{\circ}$ , showing that the paper is rotated counterclockwise at $45^{\circ}$ and upward at $90^{\circ}$ .

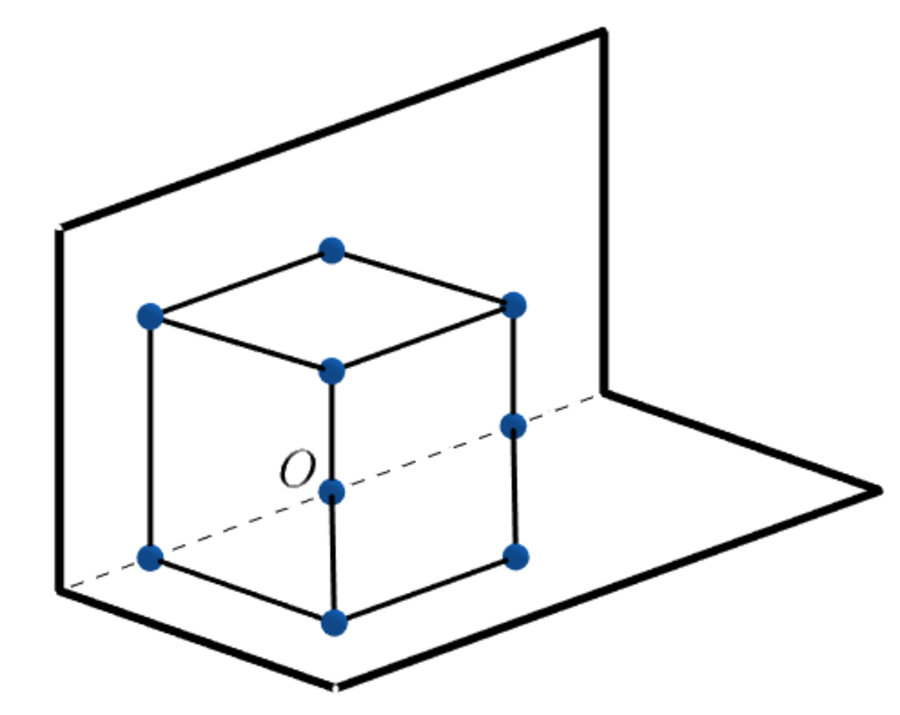
For this problem, consider the figure on the right, which illustrates the cube, containing parallel and collinear lines. The vanishing points are neglected, so that the lines do not meet at a particular point.

What can be said about the value of $\phi$ ?

Here is the video that inspires me to come up with this optical illusion problem.