Optics in Swimming Pool
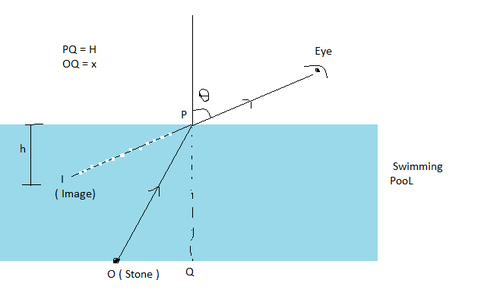 (As shown in figure) Let an Stone " O " is Placed at the bottom of swimming Pool of depth
H
and the refractive index index of water is
this stone is viewed by an man at an angle
then what will be the
apparent depth
(
h
) of this stone from water surface ?
(As shown in figure) Let an Stone " O " is Placed at the bottom of swimming Pool of depth
H
and the refractive index index of water is
this stone is viewed by an man at an angle
then what will be the
apparent depth
(
h
) of this stone from water surface ?
If the apparent depth can be expressed as :
then compute the value of .
Details and Assumption
.
are all positive integers.
This is part of my set Deepanshu's Mechanics Blasts
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Solve it independently so that you understand this question More precisely !
Concept Used in This Question Is :
∙ Formulas for Paraxial Ray's does not hold good in this question
∙ For To Locate the image we require 2 Near by rays .
∙ Position Of Image Doesn't Change if we consider to near by rays .
Now Let horizontal distance of image from Pole "P" is y
So y − x = c o n s t a n t .
Now Let Two rays of angle of incidence i & i + d i .
Now stablished relation between them ( by using snell's Law )
and use d i d ( y − x ) = 0 .
so we get
h = μ H 2 1 ( cos θ ) 3 ( H 2 + x 2 ) 2 3 .
NOTE:
Apparent depth will be maximum when we see Normally in swimming Pool.
Since θ = 0