Optics + Projectile motion + Relative motion
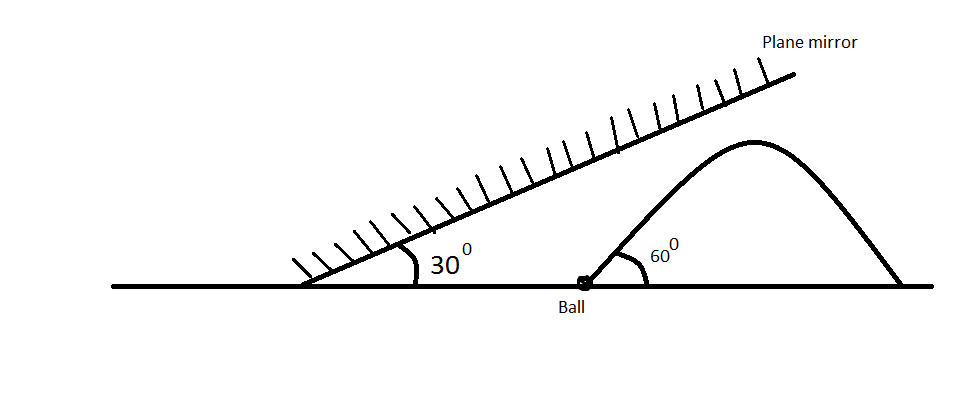 A ball is thrown with speed 20 m/s at an angle of 60 degree with the horizontal and a big plane mirror is inclined at an angle 30 degree with the horizontal as shown in the figure. Find the time at which the image of ball appears to be at rest relative to the object.
The answer is of the form (a/root b) then the value of a+b is:
A ball is thrown with speed 20 m/s at an angle of 60 degree with the horizontal and a big plane mirror is inclined at an angle 30 degree with the horizontal as shown in the figure. Find the time at which the image of ball appears to be at rest relative to the object.
The answer is of the form (a/root b) then the value of a+b is:
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
OK, the problem is a bit tricky. But first I will discuss the solution.
The image will appear relative to the ball when the velocity is perpendicular to the mirror. At the beginning, the Ball's velocity makes 6 0 0 with the horizontal while the mirror makes 3 0 0 . And that's why the ball's image will seem to be moving relative to the ball. But when the velocity makes 3 0 0 with the ground, for a moment, only for a moment, their relative velocity will be zero. Because, When you walk parallel to your dressing table mirror, you see your image still, don't you?
Now, the calculations. We have, v 0 = 2 0 m / s θ b = 6 0 0 θ m = 3 0 0 g = 1 0 m / s 2
When velocity makes 3 0 0 , Assume, Vertical component =v
Horizontal component = v 0 c o s θ b t a n θ m = v 0 c o s θ b v o r , v = v 0 c o s θ b t a n θ m
For this vertical component again, v 0 s i n θ b − v = g t o r , t = g v 0 ( s i n θ b − c o s θ b t a n θ m ) = 1 0 1 0 ( 2 3 − 2 1 3 1 ) s = 2 1 ( 3 − 2 3 1 ) s
Final job, in the b a form. = 2 1 ( 3 3 + 1 ) = 3 2
Thus, a + b = 2 + 3 = 5
You got it!