Optimal 4-Point Configuration
Let { x 1 , x 2 , x 3 , x 4 } be 4 distinct points on the Euclidian plane such that the distance between any two points is at least 1. We want to minimize the average distance beween 2 points: { x 1 , x 2 , x 3 , x 4 } ∈ R 2 min 6 1 x i , x j i < j ∑ dist ( x i , x j ) . If the minimum average distance is expressed as c a + b , where a and c are coprime and b is square-free, submit a + b + c .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
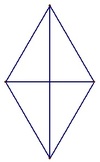 The optimal configuration has the four points at the vertices of two equilateral triangles of side
1
, so that the distances are
1
,
1
,
1
,
1
,
1
,
3
, and the average is
6
5
+
3
for a solution of
5
+
6
+
3
=
1
4
.
The optimal configuration has the four points at the vertices of two equilateral triangles of side
1
, so that the distances are
1
,
1
,
1
,
1
,
1
,
3
, and the average is
6
5
+
3
for a solution of
5
+
6
+
3
=
1
4
.
I got the answer, but how do you prove that that is the optimal configuration?
Log in to reply
Considering all rhombuses with side length 1, you get a minimal sum of diagonals in the configuration stated above.