Optimal cut
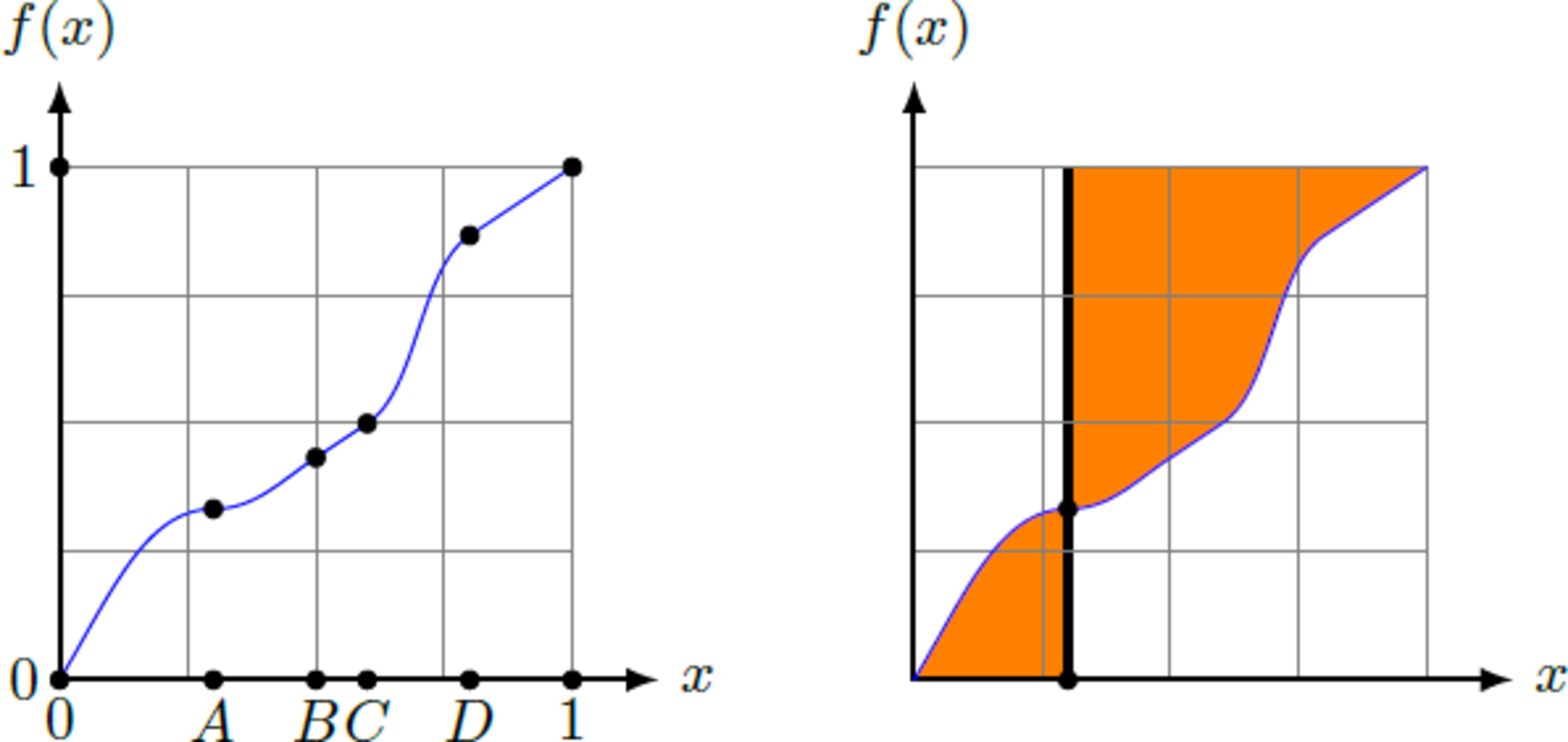
Consider the monotonically increasing function , shown below. A vertical line is drawn, which divides the graph into two parts and delimits the orange areas below and above the function. Where must the dividing line be placed in order to minimize the total orange area (in point , , or )?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For a position x = x 0 for the dividing linie we can caculate the orange area A by the integrals A ( x 0 ) = ∫ 0 x 0 f ( x ) d x + ∫ x 0 1 ( 1 − f ( x ) ) d x We zero the derivative to find the minimum A ( x 0 ) = ! min : A ′ ( x 0 ) = f ( x 0 ) − ( 1 − f ( x 0 ) ) = 2 f ( x 0 ) − 1 = ! 0 ⇒ f ( x 0 ) = 2 1 To check whether there is actually a minimum, we also calculate the second derivative A ′ ′ ( x 0 ) = 2 f ′ ( x 0 ) > 0 since the function is monotonic increasing. Therefore we found a single mimimum for f ( x 0 ) = 2 1 (point C ).