Optimal Generator Dispatch

Calculus Level 3

Suppose we have two electric generators. The amounts of power supplied by the generators are $P_1$ and $P_2$ for Generators 1 and 2, respectively. The cost per unit time to run Generator 1 is $C_1(P_1)$ , and the cost per unit time to run Generator 2 is $C_2(P_2)$ . The parentheses indicate that the cost is a function of the amount of power generated.

Suppose we want the generators to supply 100 units of power together, and minimize the running cost while doing so.

$\text{Minimize: } \hspace{0.5 cm} C_1(P_1) + C_2(P_2) \\ \text{Subject to Constraint:} \hspace{0.5 cm} P_1 + P_2 = 100$

Some plots of $\frac{dC}{dP}$ are shown below for the two generators.

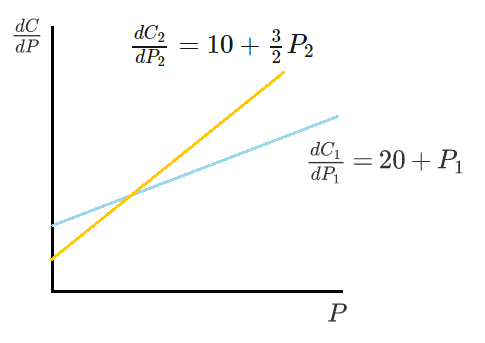
How many units of power should Generator 1 supply?

The answer is 56.

1 solution

Arjen Vreugdenhil
Nov 1, 2017

Write the total cost as a function of the amount $P$ supplied by generator 1: $C(P) = C_1(P) + C_2(100-P);$ $\frac{dC}{dP} = \frac{dC_1}{dP_1} - \frac{dC_2}{dP_2} = (20 + P_1) - (10 + \tfrac32P_2) = (20 + P) - (160 - \tfrac32 P) = \tfrac52 P - 140.$ Since this is a continuous, differentiable function on domain $P \in [0,100]$ , the minimum either lies at an edge of the domain or at the zero of $dC/dP$ .

If $P = 0$ then $dC/dP = -140$ , showing that increasing $P$ leads to a decrease in the cost; thus $P = 0$ is not a minimum.

If $P = 100$ then $dC/dP = +110$ , showing that decreasing $P$ also leads to a decrease in cost; $P = 100$ is not a minimum.

This leaves $0 = \frac{dC}{dP} = \tfrac52P - 140, \\ P = 56.$

Optimal Generator Dispatch

The answer is 56.

1 solution

0 pending reports