Optimal Power Transfer Impedance
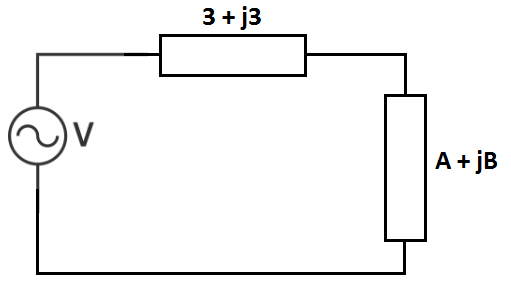
An AC voltage source with internal impedance feeds a load with a complex impedance of .
If and are chosen so as to maximize the active power transferred to the load, what is ?
Clarification: .
Bonus: Can you prove the generalization of this?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the internal impedance of the AC voltage source be Z i = ( a + j b ) Ω and Z L = ( A + j B ) Ω . Then, the load current is given by:
I ∠ ϕ ⟹ ϕ = Z i + Z L V ∠ 0 = a + b + j ( A + B ) V = ( a + A ) 2 + ( b + B ) 2 ∠ tan − 1 a + A b + B V = − tan − 1 a + A b + B
The active power transferred to the load is maximum when the power factor cos ϕ is maximum.
cos ϕ = cos ( − tan − 1 a + A b + B ) = cos ( tan − 1 a + A b + B ) = 1 + ( a + A b + B ) 2 1
Note that cos ϕ is maximum when B = − b and cos ϕ = 1 .
When B = − b , then Z i + Z L = a + A . Then the equivalent circuit is the AC voltage source is series with its internal resistance R i = a and load resistance R L = A and maximum active transferred to the load is when R L = R i or A = a (see Note ).
Therefore, the active power transferred to the load impedance is maximum when A = a and B = − b and when a = b = 3 , A + B = 3 − 3 = 0 .
Note: Consider a voltage source V with internal resistance r in series with a load resistance R . Then the load current is I = r + R V and the power transferred to R is given by:
P = V R I = r + R R V × r + R V = ( r + R ) 2 R V 2 = R r 2 + 2 + R V 2
P is maximum, when R r 2 + R is minimum. By AM-GM inequality R r 2 + R ≥ 2 r . Equality occurs when R = r . Therefore, maximum power transferred occurs when load resistance equals to internal resistance.