Optimal shot on goal
In a soccer match, the striker ( point S ) has beaten all defenders and is running parallel to the sideline towards the goal line. At what distance x from the goal line should the striker shoot at the goal for the best chance of a goal? Give the result in meters and round to one decimal place.
Details and Assumptions:
- The striker will shoot the ball in a straight line on the ground.
- The striker isn't perfectly accurate, so his shot may be slightly off from where he intends.
The answer is 19.3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
The final result is sqrt(s(s+w)), not sqrt(w(w+s))
Log in to reply
You are right, this is a typo. Sometimes, when I code in TeX I get obvious things wrong. But thanks to your comment, I could correct my solution.
Will it be easier if you use cot instead of tan since you don't need to do a complex chain rule for x? (the answer is still the same) ε = a r c c o t ( s + w x ) − a r c c o t ( s x )
Not sure what I'm looking at here, but I think I like it. What's the rationale?
Log in to reply
Sorry my explanation it was sketchy, sometime I feel I could be lecturing what I do not want to. I include two more detailed drawings, from where you can get the whole picture even for an arbitrary path of the striker. I ask you consider the following facts 1) From any circumference passing over two point A and B you see the segment AB under same angle
Gud u proved it geometrically
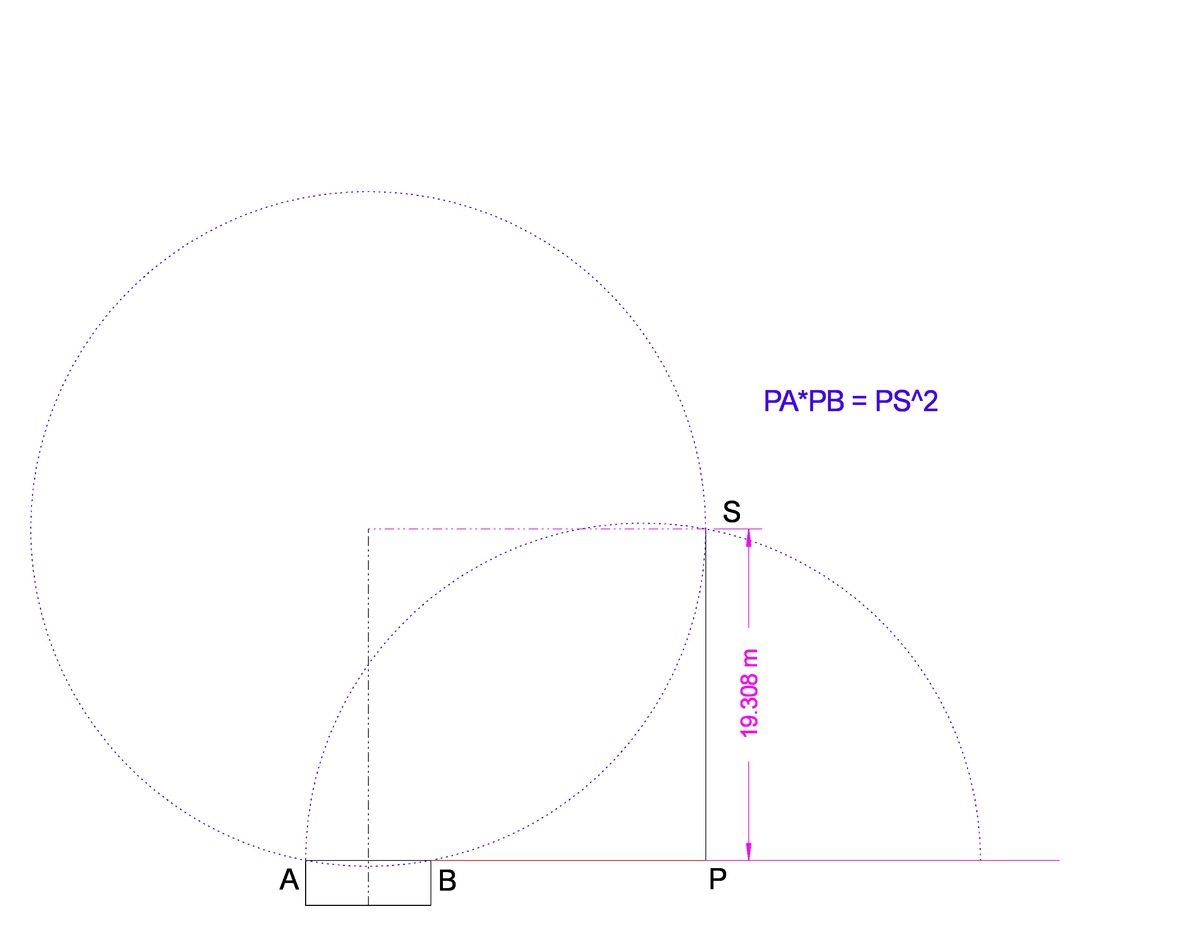
Actually we are intending to find the maximun angle you can face the segment AB from line SP. This point must be in the circunference containing A and B and being tangent to line SP. Other circunference will have to points of intersection with SP and the angle will be smaller, compare it among all the isosceles triangle of base AB. The drawing is just the graphical construction of such circunference using polarity. For clarity I maybe should have named as B1 the point symetrical to B with respect to P. Then the diameter of semicircunference is AP+PB and so the its intersection with PS give us the tangency point, which the point we are looking for.
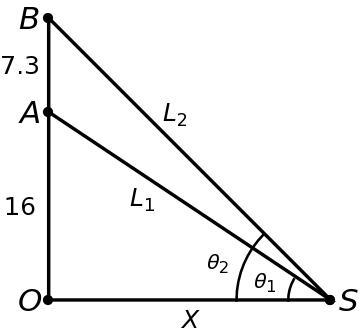
This solution has a similar basis as the one Markus provided. I did not want to take derivatives of trigonometric functions, though, so I used some tricks to get rid of them. I assume θ 1 , θ 2 are the angles to the corners of the goal with respect to the side of the pitch and L 1 , L 2 are the distances to the same corners. The quantity that needs maximized is θ 2 − θ 1 . Because sin ( θ 2 − θ 1 ) follows the same trend over the domain of interest, that function can be used instead. Employing the rules of addition/subtraction for the sine function,
sin ( θ 2 − θ 1 ) = sin ( θ 2 ) cos ( θ 1 ) − cos ( θ 2 ) sin ( θ 1 ) = L 2 2 3 . 3 ⋅ L 1 x − L 2 x ⋅ L 1 1 6 = L 1 L 2 7 . 3 x
L 1 L 2 = ( x 2 + 1 6 2 ) ( x 2 + 2 3 . 3 2 ) = x 4 + 2 ( 1 6 2 + 2 3 . 3 2 ) x 2 + ( 1 6 ⋅ 2 3 . 3 ) 2
We need to maximize this quantity with respect to x , so taking its derivative and solving for zero. Using a generalized equation,
d x d ( x 4 + b x 2 + c a x ) = ( x 4 + b x 2 + c ) 3 / 2 a ( x 4 − c )
x can be solved for by setting x 4 − c = 0 .
x 4 − ( 1 6 ⋅ 2 3 . 3 ) 2 = 0 x = ( 1 6 ⋅ 2 3 . 3 ) 1 / 2 x = 1 9 . 3 0 8 . . .
Draw any circle through the two goals posts (
P
1
,
P
2
), and put the striker
S
on that circle (to the right of the goal line). The view angle of the goal for the striker (
∠
P
1
S
P
2
) is independent of the location of the striker on that circle (a geometry theorem). Furthermore, it varies inversely with the radius of the circle: smaller circle gives larger view angle. So, we are looking for the smallest circle through the goal posts and the striker. This is a circle that touches the sideline on which the striker is located, and its center is located on the perpendicular bisector of the goal posts. Hence, the radius of that circle equals
1
6
+
7
.
3
/
2
=
1
9
.
6
5
. See diagram:
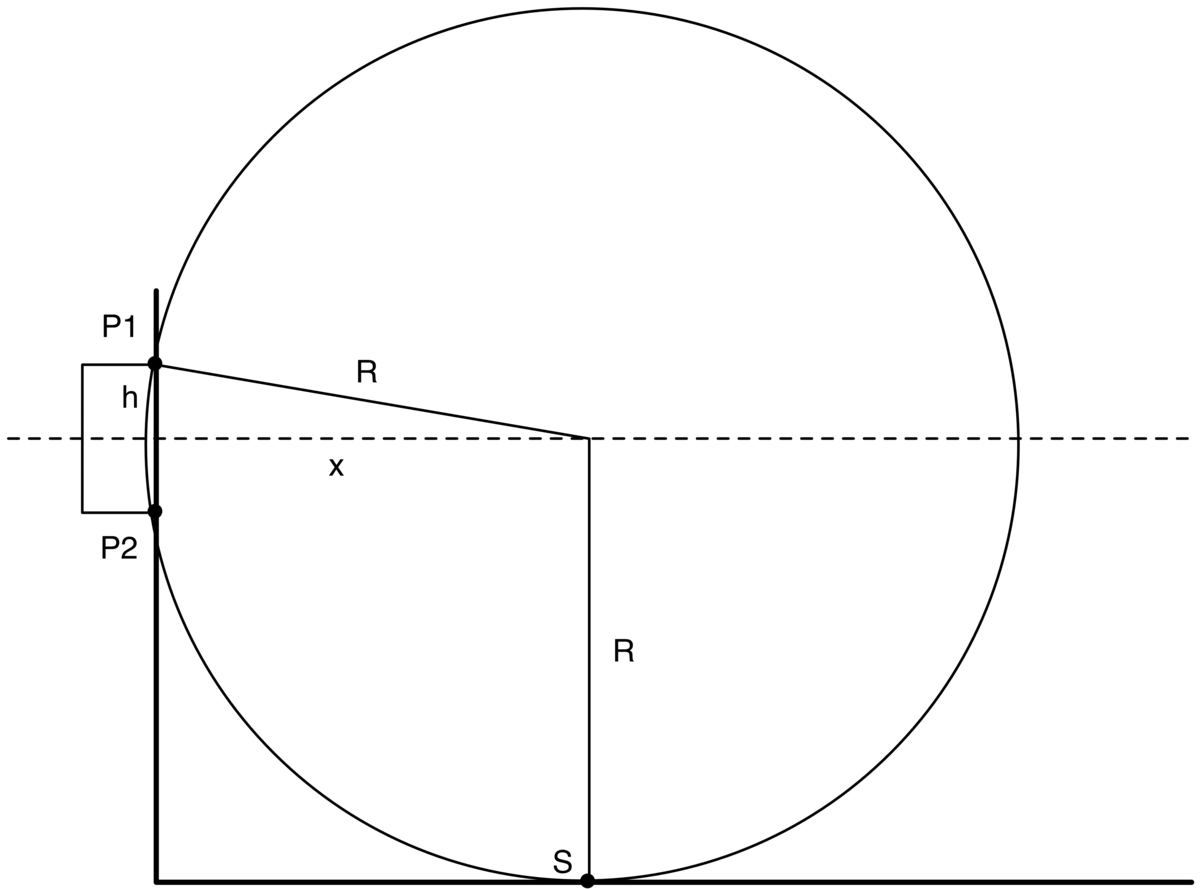
Therefore, we have x 2 + 3 . 6 5 2 = 1 9 . 6 5 2 , and thus x = 1 9 . 6 5 2 − 3 . 6 5 2 ≈ 1 9 . 3 0 8 .
I did y= (tan^-1(16/x))-(tan^-1(23.3/x)) and looked for the max value when it was graphed which turned out to be 19.311 Done by a highschool kid with a C+ in trig
We want the angle from the player to the goal to be largest, which can be written as
θ = t a n − 1 ( x 2 3 . 3 ) − t a n − 1 ( x 1 6 )
Now combine the two arctans:
t a n ( θ ) = t a n ( t a n − 1 ( x 2 3 . 3 ) − t a n − 1 ( x 1 6 ) )
= 1 + x 2 3 . 3 x 1 6 x 2 3 . 3 − x 1 6
= x 2 + ( 2 3 . 3 × 1 6 ) 7 . 3 x
If we want to maximise θ, we just maximise tan(θ). Therefore we just solve
d x d x 2 + ( 2 3 . 3 × 1 6 ) 7 . 3 x = 0
⇒ x = 1 9 . 3 0 8 0 . . .
At the last step, you could have also taken the reciprocal of the fraction and used AM-GM to minimize it, instead of using calculus.
If we let a = 1 6 , b = 1 6 + 7 . 3 and the angle be θ combining trig and Pythagoras we can get: cos θ = ( x 2 + a 2 ) ( x 2 + b 2 ) x 2 + a b = ( a b ) ( ( a x 2 + a ) ( b x 2 + b ) ) x 2 + a b
And using AM-GM: cos θ ≥ a b 2 ⋅ a x 2 + b x 2 + a + b x 2 + a b = a b 2 ⋅ a + b a b = a + b 2 a b
As cos θ is decreasing as θ is increasing this corresponds to the maximum value of θ . Equality is when x = a b = 1 9 . 3
Using the Law of Sines, we have
S i n ⎝ ⎛ A r c S i n ⎝ ⎛ x 2 + ( 1 6 + 7 . 3 ) 2 x ⎠ ⎞ ⎠ ⎞ x 2 + 1 6 2 = S i n ( θ ) 7 . 3
where θ is the angle the goal posts present to the striker, which we wish to maximize. Since for small θ the right side is a monotonic, we only need to find x such that the following has the minimum value for the maximum θ
x 1 x 2 + 1 6 2 x 2 + ( 1 6 + 7 . 3 ) 2
which occurs when x = 1 9 . 3 0 8 . . .
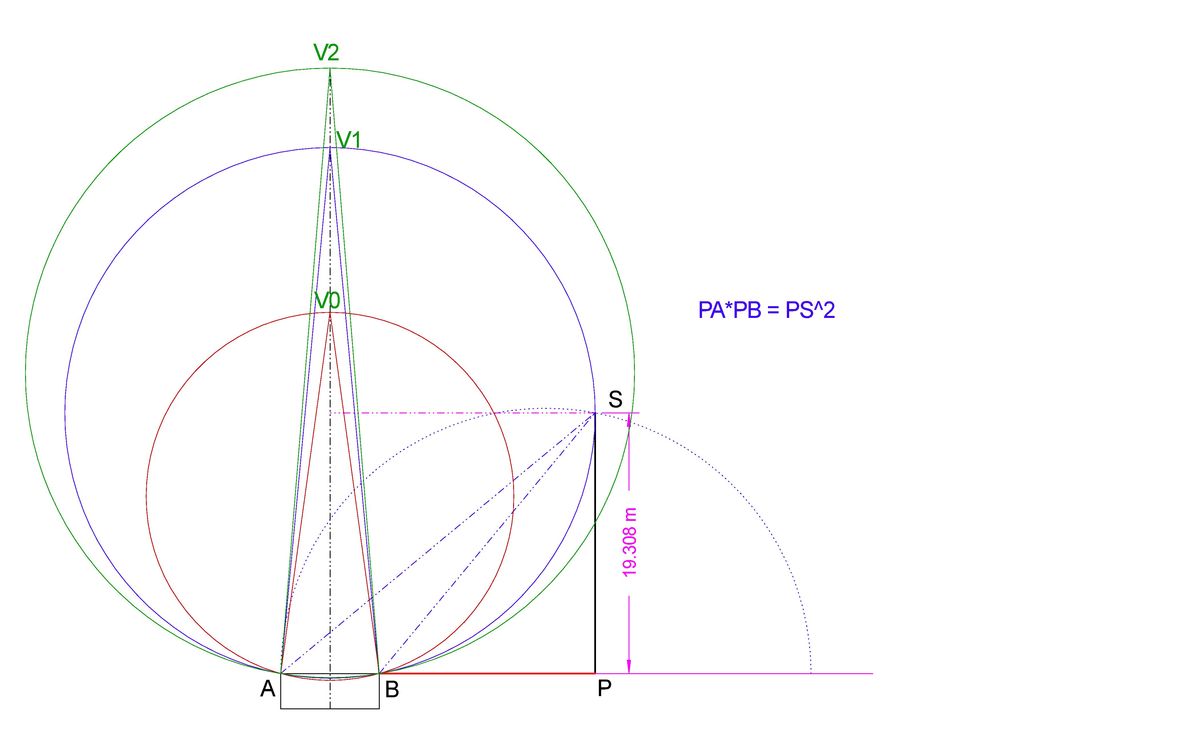
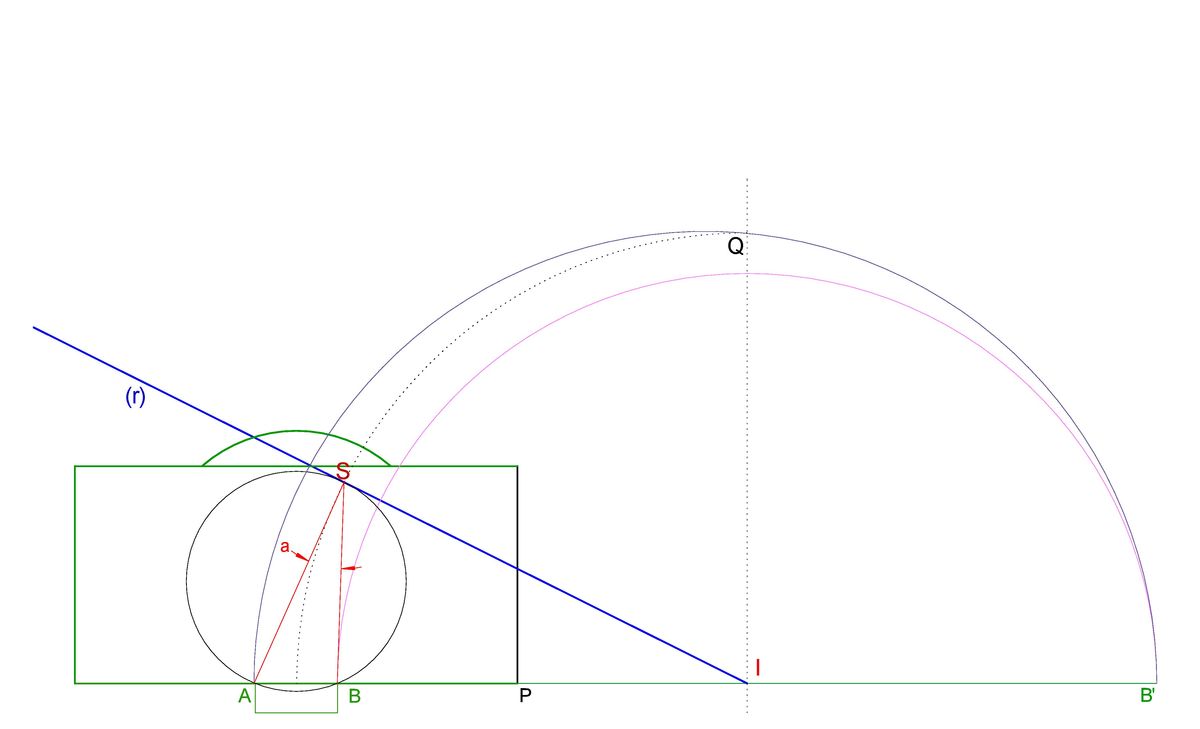
We consider the triangle formed by the point S (striker) and the points A and B (goal post). The best chance to score has the striker when the opening angle ϵ becomes maximal. This is true even if the goalkeeper tries to cover the space between striker and goal, because at maximum angle ϵ also the distance between the goalkeeper and the ball's path becomes maximum. (This is especially true when the ball is played against the running direction of the keeper.)
The length s = 1 6 m und w = 7 . 3 m are the distance to goal post and the width of the goal, respectively. The angles are determined by tan ( α ) tan ( α + ε ) ⇒ ε = x s = x s + w = arctan ( x s + w ) − arctan ( x s ) With arctan ′ ( y ) = 1 + y 2 1 the derivative results ⇒ ⇒ ⇒ ⇒ d x d ε = 1 + ( x s + w ) 2 − x 2 s + w − 1 + ( x s ) 2 − x 2 s x 2 + ( s + w ) 2 s + w s ( x 2 + ( s + w ) 2 ) − w x 2 x = ! 0 = x 2 + s 2 s = ( s + w ) ( x 2 + s 2 ) = − w ( w + s ) s = s ( w + s ) ≈ 1 9 . 3 m Therefore, the result is the geometric mean between the distances s and s + w between the striker and the goal posts along the goal line.