Optimal Tetrahedron

If the normal to the new plane is $\mathbf{u}$ , where all three components of $\mathbf{u}$ are positive, then the equation of the new plane is $\mathbf{r} \cdot \mathbf{u} = u_1a + u_2b + u_3c$ , and to the intercepts of the new plane with the $x$ -, $y$ - and $z$ -axes are $(\tfrac{u_1a+u_2b+u_3c}{u_1},0,0)$ , $(0,\tfrac{u_1a+u_2b+u_3c}{u_2},0)$ and $(0,0,\tfrac{u_1a+u_2b+u_3c}{u_3})$ , and so the volume of the tetrahedron is $V = \frac{(u_1a+u_2b+u_3c)^3}{6u_1u_2u_3}$ Using the Arithmetic-Geometric Mean Inequality, we have $\frac{u_1a + u_2b + u_3c}{3} \; \ge \; \sqrt[3]{u_1u_2u_3abc}$ and hence $\frac{(u_1a+u_2b+u_3c)^3}{u_1u_2u_3} \; \ge \; 27abc$ and hence $V \ge \boxed{\tfrac92abc}$ , with equality when $\mathbf{u}$ is parallel to $a^{-1}\mathbf{i} + b^{-1}\mathbf{j} + c^{-1}\mathbf{k}$ .

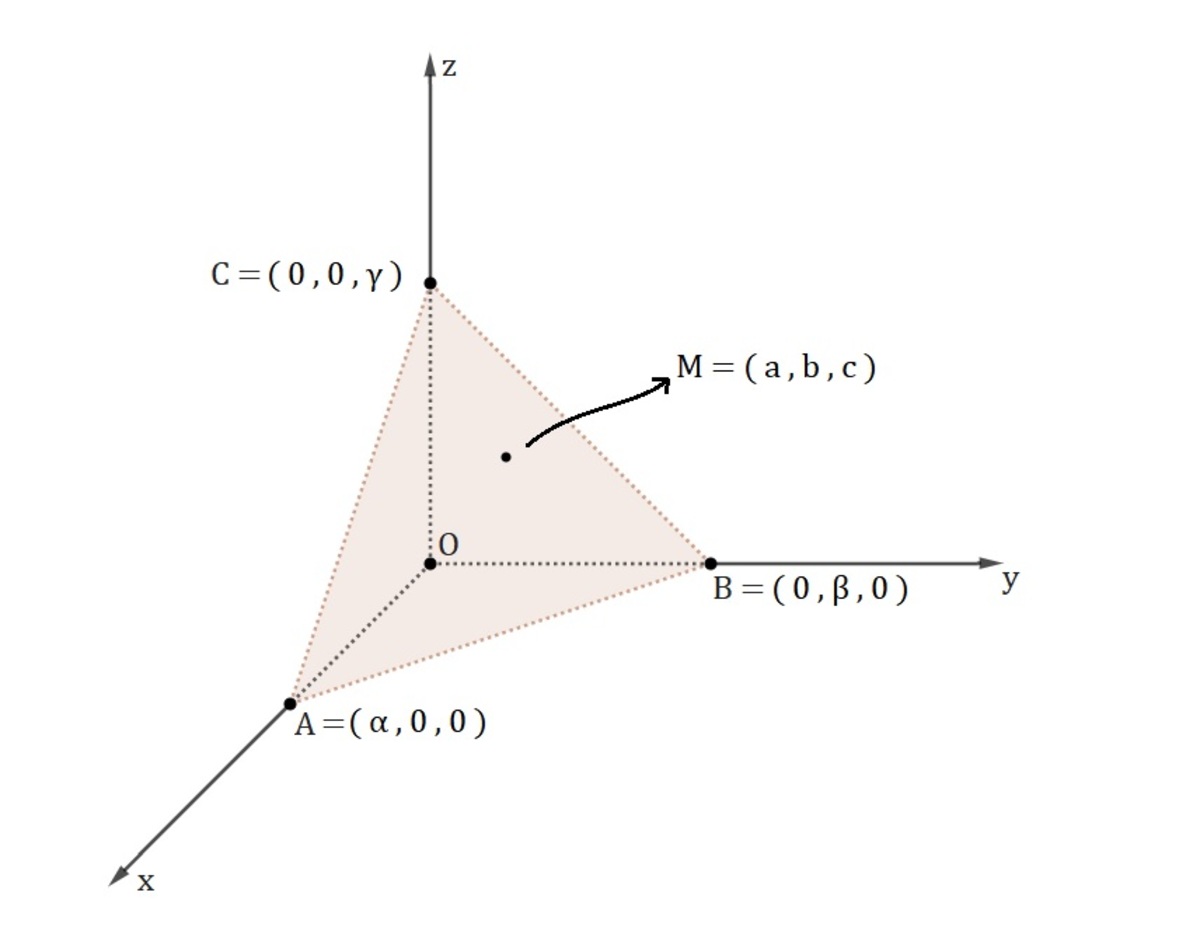
In the image above we have a representation of the problem. We have some plane that cut the coordinate axes at points $A$ , $B$ and $C$ . It forms a "right" tetrahedron $OABC$ . The point $M=(a,b,c)$ is in that plane.

The equation of this plane can be written as $\displaystyle{\frac { x }{ \alpha } +\frac { y }{ \beta } +\frac { z }{ \gamma } =1}$ . The volume of the tetrahedron $OABC$ is given by $\displaystyle{\frac { \alpha \beta \gamma}{ 6 } }$ .

If the point $M$ is in the plane, we can write the plane equation as $\displaystyle{\frac { a }{ \alpha } +\frac { b }{ \beta } +\frac { c }{ \gamma } =1}$ .

Now our problem is to optimize the volume function giving the plane equation as a constraint.

We can use Lagrange Multipliers .

Setting $\displaystyle{g(\alpha,\beta,\gamma)=\frac { a }{ \alpha } +\frac { b }{ \beta } +\frac { c }{ \gamma } =1}$ and $\displaystyle{f(\alpha,\beta,\gamma)=\frac { \alpha \beta \gamma}{ 6 }}$ , we have:

$\displaystyle{\nabla f = \left(\frac {\beta \gamma}{ 6 },\frac { \alpha \gamma}{ 6 },\frac { \alpha \beta }{ 6 }\right)}$

$\displaystyle{\nabla g = \left(-\frac {a}{ {\alpha}^2 },-\frac {b}{ {\beta}^2 },-\frac {c }{ {\gamma}^2 }\right)}$

We need $\displaystyle{\nabla f = \lambda \nabla g}$ , so:

$\displaystyle{\left(\frac {\beta \gamma}{ 6 },\frac { \alpha \gamma}{ 6 },\frac { \alpha \beta }{ 6 }\right)=\lambda \left(-\frac {a}{ {\alpha}^2 },-\frac {b }{ {\beta}^2 },-\frac {c }{ {\gamma}^2 }\right)}$

Finally, we need to solve the following system of equations:

$\displaystyle{\begin{cases} \frac { a }{ \alpha } +\frac { b }{ \beta } +\frac { c }{ \gamma } =1\quad (1) \\ \frac { \beta \gamma }{ 6 } =-\frac { -\lambda a }{ { \alpha }^{ 2 } } \quad (2) \\ \frac { \alpha \gamma }{ 6 } =-\frac { \lambda c }{ { \beta }^{ 2 } } \quad (3) \\ \frac { \alpha \beta }{ 6 } =-\frac { \lambda c }{ { \gamma }^{ 2 } } \quad (4) \end{cases}}$

Multiplying equations $(2)$ , $(3)$ and $(4)$ by $\alpha$ , $\beta$ and $\gamma$ respectively:

$\displaystyle{(2)'\quad \frac { \alpha \beta \gamma }{ 6 } =-\frac { \lambda a }{ { \alpha } }}$

$\displaystyle{(3)'\quad \frac { \alpha \beta \gamma }{ 6 } =-\frac { \lambda b }{ { \beta } } }$

$\displaystyle{(4)'\quad \frac { \alpha \beta \gamma }{ 6 } =-\frac { \lambda c }{ { \gamma } } }$

Adding up these equations and using the equation $(1)$ we will get:

$\displaystyle{\frac { \alpha \beta \gamma }{ 2 } =-\lambda \left(\frac { a }{ { \alpha } }+\frac { b }{ { \beta } }+\frac { c }{ { \gamma } }\right)}$

$\displaystyle{\boxed{\lambda =-\frac { \alpha \beta \gamma }{ 2 }}}$

Using this result back on the equations $(2)$ , $(3)$ and $(4)$ we will get:

$(2)$ :

$\displaystyle{\frac { \beta \gamma }{ 6 } =\frac { a\alpha \beta \gamma }{ 2{ \alpha }^{ 2 } } }$

$\displaystyle{\frac { 2\alpha}{ 6 } =a}$

$\displaystyle{\boxed{\alpha=3a}}$

$(3)$ :

$\displaystyle{\frac { \alpha \gamma }{ 6 } =\frac { b\alpha \beta \gamma }{ 2{ \beta }^{ 2 } } }$

$\displaystyle{\frac { 2\beta}{ 6 } =b}$

$\displaystyle{\boxed{\beta=3b}}$

$(4)$ :

$\displaystyle{\frac { \alpha \beta }{ 6 } =\frac { c\alpha \beta \gamma }{ 2{ \gamma }^{ 2 } } }$

$\displaystyle{\frac { 2\gamma}{ 6 } =c}$

$\displaystyle{\boxed{\gamma=3c}}$

These results tell us that the volume of the tetrahedron will be optimal when the equation of the plane is $\displaystyle{\frac { x }{ 3a } +\frac { y }{ 3b } +\frac { z }{ 3b } =1}$ . The volume of the tetrahedron will be $\displaystyle{\frac {3a3b3c }{ 6 } =\boxed{\frac {9abc }{ 2 }}}$ .

The reason that this volume is minimum can be observed imagining a plane that is parallel to the plane $z=0$ . The volume would be infinity. The this plane is tilted until it becomes parallel to the Z axis. The volume is still infinity. So, this solution must be point of minimum.