Optimise the number of coins a boat can hold
Uncle Bob has a square piece of paper of side length and he tries to fold margins of width on each side in order to maximize the number of coins the resulting boat can hold. The boat created must be a cuboid with a square base (of side length ), as illustrated below.
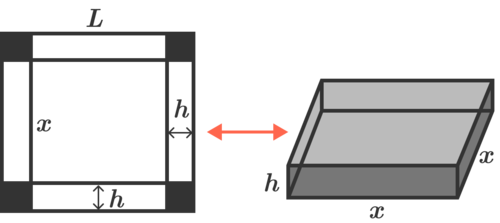 Paper boat construction
Paper boat construction
When constructing the boat, Bob must use the whole surface of the paper, so the corners colored in black must be folded (not cut). Then, Bob submerges the boat in water and puts a certain number of coins in it. To his surprise, he notices that when changing the width of the margins folded, , the number of coins the boat can hold changes as well. Now Bob wants to find out how many of these his prototype can support, but he doesn't quite remember anything from his physics lessons in school, so he needs your help!
Your task is to find the maximum number of coins such a boat can hold, rounded to the nearest multiple of . Assume that the coins are quasi-punctiform and that only their weight matters towards deciding whether the boat can hold them or not. You are given the following:
- The mass of a single coin is
- The areal density of the paper is
- The density of water is and gravity is
The answer is 1840.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Setup. In order for the boat to remain in equilibrium and to maximise the number of coins, it must be (almost) fully submerged in water. Therefore, we can claim that B + W = 0 , where B is buoyancy and W = W b + W c , the weight of the boat + the weight of the coins
Expressing each term individually, we get ρ V g = m b g + N m g ⟹ N = ⌊ m ρ V − m b ⌋
The mass of the boat is given by m b = σ L 2 , because we are given the areal density of the paper, and we're left with N = ⌊ m ρ V − σ L 2 ⌋ ( 1 )
From this expression, we can assess that as V grows, N must grow too. So it's all about maximising the volume!
When is the volume maximal? First, let's express the volume as a function of two parameters, L and h . Looking at the scheme in the problem body, it is easy to establish that
V ( h , L ) = ( L − 2 h ) 2 h = 4 h 3 − 4 L h 2 + L 2 h
Now, we know that a derivative expresses the rate of change of a function's output for certain values of its parameters. Keeping that in mind, we can deduce that when a function reaches its maximal value, its derivative must be 0 , as it cannot increase any further. However , this also happens when the function reaches its minimal value, as it cannot decrease any further. That being said, we aim to compute the derivative of V with respect to h , and setting it to be 0 , then being careful about which of the solutions of the obtained polynomial fulfils the necessary criteria for the volume to be maximal.
∂ h ∂ V = ∂ h ∂ ( 4 h 3 − 4 L h 2 + L 2 h ) ∂ h ∂ V = ∂ h ∂ ( 4 h 3 ) + ∂ h ∂ ( − 4 L h 2 ) + ∂ h ∂ ( L 2 h ) ∂ h ∂ V = 1 2 h 2 − 8 L h + L 2
Imposing the extremum condition, then solving the quadratic yields:
∂ h ∂ V = 0 ⟹ 1 2 h 2 − 8 L h + L 2 = 0 ⟹ h ∈ { 2 L , 6 L }
But 2 L is definitely not the solution we were seeking, as the volume in that case would be 0 , so we're left with
h = 6 L ⟹ V = 2 7 2 L 3 ( 2 )
From relations ( 1 ) and ( 2 ) , we can infer that
N = ⌊ m ρ 2 7 2 L 3 − σ L 2 ⌋ N = ⌊ m L 2 ( 2 7 2 ρ L − σ ) ⌋
Calculating with the given values, N ≈ ⌊ 1 8 4 1 . 8 5 ⌋ , and rounded to the nearest multiple of 1 0 , we get our answer, 1 8 4 0 .