Optimizing velocity in an elastic collision?
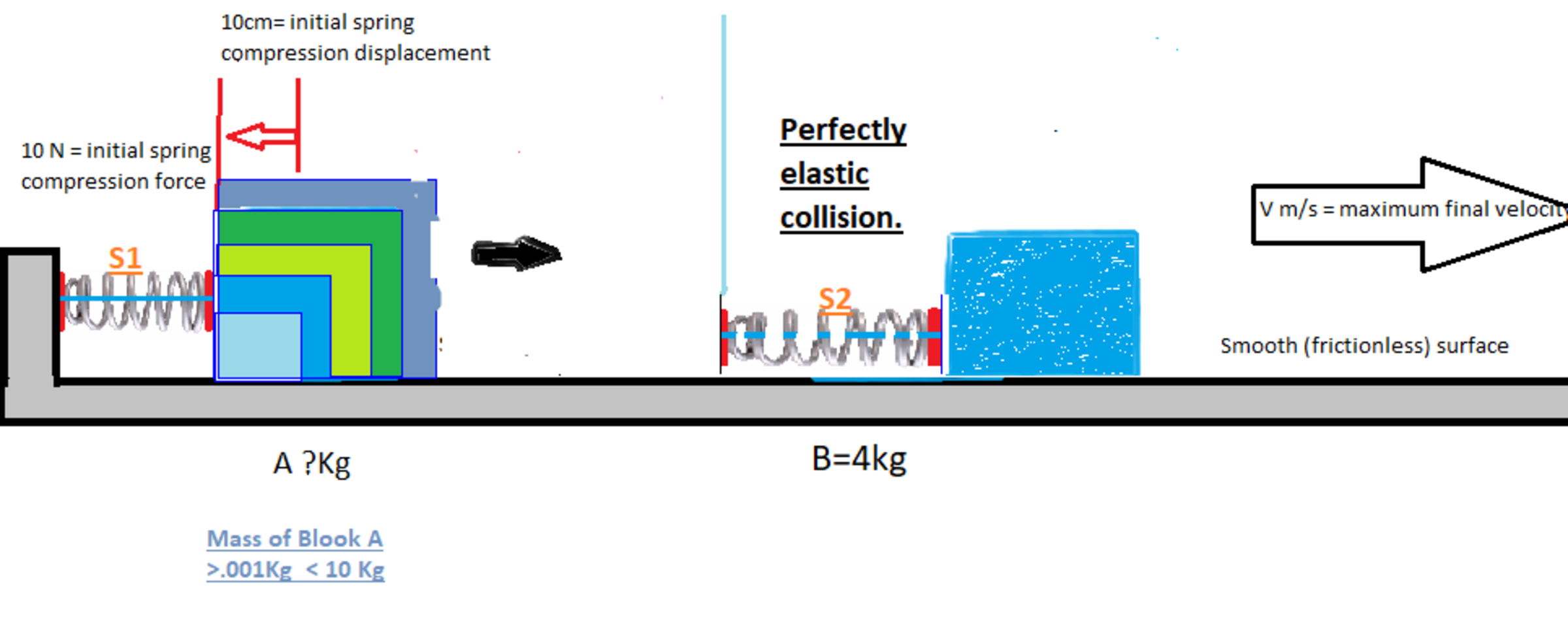
Determine the maximum possible velocity of block B. = V (m/s)
Determine the mass of block A required to achieve maximum velocity of block B. = M(kg)
Give your answer as V * M.
Block B will be set in motion as a result of block A colliding with spring S2. Block A will be set in motion as a result of the release of the mechanism that is initially holding the spring S1 in compression.
Assumptions and givens.
Initial force to hold spring S1 = 10 newtons
Initial compression displacement of spring S1 = 10cm
Mass of block B =4Kg
The mass of block A can be selected to any value that is greater than 1 gram and less than 10 Kg.
The two blocks are resting motionless on a smooth rail as indicated in the diagram.
Block A is initially siting against a compressed spring S1.
Block B is located at a distance so that Block A will be completely clear of spring S1 before any contact is made with spring S2
The springs are linear springs where the compression force is directly proportional to the compression displacement.
The collision of block A with B is cushioned by spring S2 resulting in a perfectly elastic collision.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Potential energy in the compressed spring. E s = 2 1 k x 2
Hooke’s law F = k x or k = F / x
E s = 2 1 x F x 2 E s = 2 1 F x E s = 2 1 1 0 ∗ 0 . 1 E s = 0 . 5 J
Kinetic energy E k = 2 1 m v 2
Initially both blocks have 0 velocity. No kinetic energy.
All the springs potential energy is transferred to Kinetic energy in the movement of Block A. E s = E k 0 . 5 j = 2 1 m A v A 2
An elastic collision conservation of momentum and conservation of energy are observed.
The total kinetic energy of the two blocks will remain constant before and after the collision between the blocks. Each block may have some velocity and therefor some portion of the total kinetic energy. Kinetic energy is proportional to the square of the velocity. Even a negative value of velocity will result in a positive value for the kinetic energy for that block. Since it is not possible to have a negative value for the kinetic energy for a block, zero kinetic energy is the smallest possible value that can be achieved. The goal is to achieve the highest possible velocity for block B. The highest conceivable amount of energy that could be transferred to block B in the collision would be all the energy that is in the system. . If all the energy is transferred to block B in the collision, then block A would have zero kinetic energy ie zero velocity.
E A _ b e f o r e = E B _ a f t e r E B _ a f t e r = 0 . 5 j 0 . 5 j = 2 1 m b v B _ a f t e r 2 m b = 4 k g V B _ a f t e r = 2 4 1 = 0 . 5 s m
All elastic collisions conserve the total kinetic energy and momentum. only under certain specific circumstances will the Kinetic energy and momentum of the two colliding masses swap.
During an elastic collision there is a deformation or compression that occurs between the two masses. The elastic compression may occur in either one of or both masses, in the cases of this problem it occurs in spring S2. After the initial impact the spring S2 begins to be compressed. The left end of S2 will be pushing left on block A while the right end of the spring is pushing right on block B. Through the entire impact event the forces applied to each block by the spring will be equal in magnitude and opposite in direction for the same length of time. F=ma can by applied to the movements of each mass. Block A will be de-accelerating and block B will be accelerating under the influence of identical forces for the entire impact event. The magnitude of the forces acting on the blocks are equal and the time that the forces are applied to each block are equal then only the magnitude of the mass of each block is left to influence the acceleration rates. A=f/m, larger mass will result in a smaller magnitude of acceleration. Only when the mass of the two blocks are equal will the acceleration magnitude be equal for each of the blocks. Any circumstance where the blocks are not of equal mass will result in the more massive block accelerating at lower rate. That imbalance in acceleration rate will result in a greater portion of the change in initial velocities being experienced by the block with less mass.
Only when the mass of the two blocks are equal will the elastic collision result in block A having a final velocity equal to block B’s initial velocity and vice versa. m A = m B m A = 4 k g )
Answer m A v B = 4 ∗ 0 . 5 = 2
There are numerous games and sports where the properties of colliding objects of equal mass can be observed. Pool, curling, croque would be examples, amongst many others. It is common practice to take advantage of the exchange of momentum and energy between to equal mass objects in near elastic collisions.
Newton’s cradle might be considered a somewhat applicable demonstration of the reactions and results of masses of various magnitude colliding at various velocities.
Let the velocity of block A before collision be v A , i , and after collision be v A , f . Then 2 1 M v A , i 2 = 2 1 × 1 0 × 0 . 0 1 = 0 . 5 . Since the collision is perfectly elastic, therefore M v A , i = M v A , f + 4 V , and 2 1 M v A , i 2 = 2 1 M v A , f 2 + 2 1 × 4 × V 2 . These yield 2 M v A , i = ( M + 4 ) V or V = M + 4 2 M v A , i = 4 v A , i 2 + 1 2 v A , i ≤ 2 1 . The equality holds when 2 v A , i = 2 v A , i 1 or v A , i = 2 1 and hence M = 4 . Therefore V × M = 0 . 5 × 4 = 2