Optimizing velocity in inelastic collision?
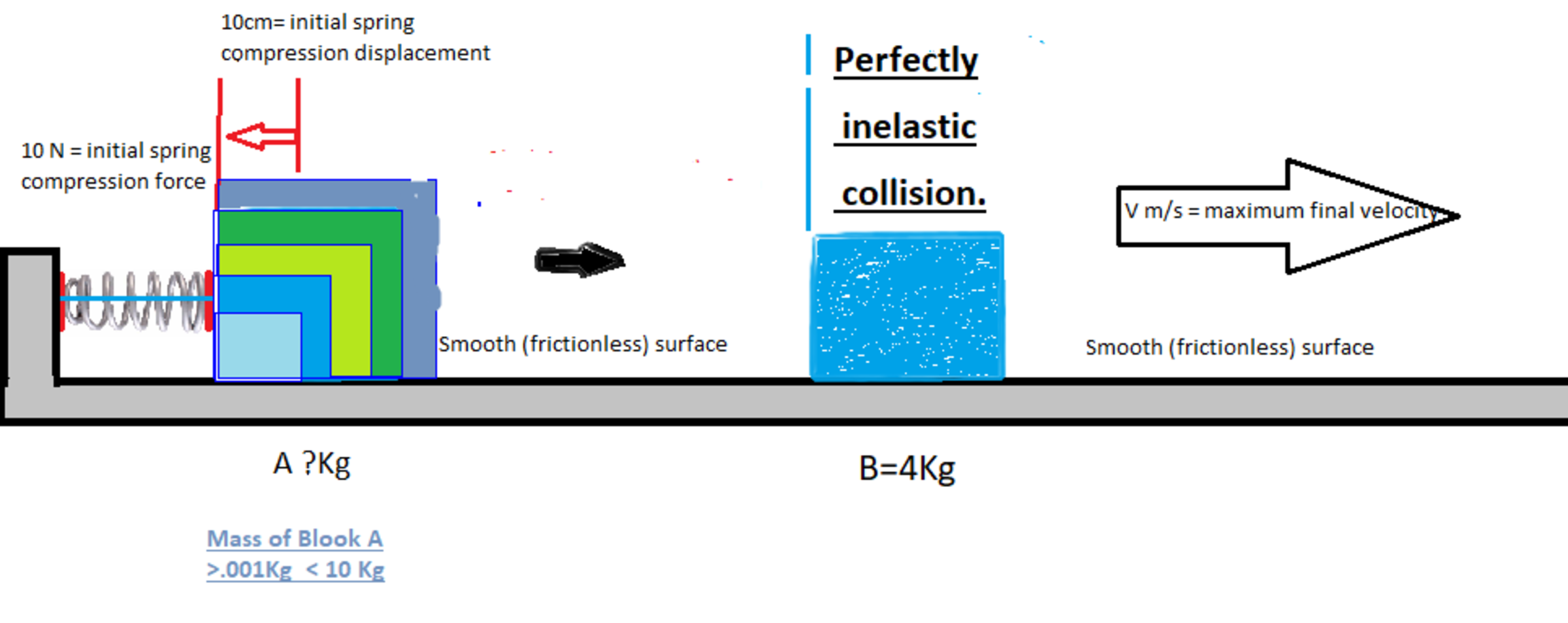
Determine the maximum possible velocity of block B. = V (m/s)
Determine the mass of block A required to achieve maximum velocity of block B. = M(kg)
Give your answer as V * M.
Block B will be set in motion as a result of block A colliding with block B. Block A will be set in motion as a result of the release of the mechanism that is initially holding the spring S1 in compression.
Assumptions and givens.
Initial force to hold spring S1 = 10 newtons
Initial compression displacement of spring S1 = 10cm
Mass of block B =4Kg.
The mass of block A can be selected to any value that is greater than 1 gram and less than 10 Kg.
The two blocks are resting motionless on a smooth rail as indicated in the diagram.
Block A is initially siting against a compressed spring.
Block B is located at a distance so that Block A will be completely clear of spring before any contact is made with block B.
The spring is a linear spring where the compression force is directly proportional to the compression displacement.
The collision of block A with B is a perfectly inelastic collision i.e. no bounce at all between the blocks after they collide.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Potential energy in the compressed spring. E s = 2 1 k x 2
Hooke’s law F = k x or k = F / x
E s = 2 1 x F x 2 E s = 2 1 F x E s = 2 1 1 0 ∗ 0 . 1 E s = 0 . 5 J
Kinetic energy E k = 2 1 m v 2
Initially both blocks have 0 velocity. No kinetic energy.
All the springs potential energy is transferred to Kinetic energy in the movement of Block A.
E s = E k 0 . 5 j = 2 1 m A v A 2 v A − b e f o r e = 2 m A 1
An inelastic collision conservation of momentum is observed. Energy will be lost to deformation of the blocks, vibrations, noise, heat etc. after the collision both blocks will be moving at the same velocity with no separation between them.
The total mass moving towards the right will be the sum of the two blocks.
v A − a f t e r = v B − a f t e r v B − b e f o r e = 0
Momentum = mass time velocity.
( p = m v p A − b e f o r e + p B − b e f o r e = p A − a f t e r + p B − a f t e r m A v A − b e f o r e + m B v B − b e f o r e = m A v A − a f t e r + m B v B − a f t e r m A 2 m A 1 + 0 = m A v A − a f t e r + 4 v B − a f t e r m A 2 m A 1 = ( m A + 4 ) v B − a f t e r v B − a f t e r = m A 2 m A 1 / ( m A + 4 ) ) v B − a f t e r = ( m A + 4 ) 2 m A
Equation relates the velocity of block B after the collision as it relates to the mass of block A.
The problem has become; determine the value of mass for block A that returns the largest value for velocity of block B in this expression. It has been more that 40 years since I have done any calculus, I don’t recall much. I believe the solution would be to find the first derivative of this relatively simple expression and then equate that first derivative (slop of the line) to = 0. I decided to leave that to someone that is more comfortable with calculus.
I took the practical route (for me). I took a couple of minutes, inserted the expression in a excel spreadsheet and had the excel solver determine the highest possible value for the velocity.
It seems to me that there may be some question as to whether anyone will ever read this post but if someone has a different approach I would very much like to see it.
Maximum value for Velocity of block B is 0.25m/s
The mass of block A that is required to achieve that maximum velocity = 4kg
Not unexpected, the mass of block A must equal the mass of block B in order to achieve the maximum velocity after the collision.
Answer
m A v B = 4 ∗ 0 . 2 5 = 1
It is given that the stretch of the spring is 0 . 1 m. and the spring force is 1 0 N. So the force constant of the spring is 1 0 0 N/m. Energy stored in the spring is 2 1 × 1 0 0 × ( 0 . 1 ) 2 = 0 . 5 Joules. So velocity acquired by the block A is u = M 1 . Since the collision is perfectly inelastic, the two blocks will move together with velocity v obtained from the momentum conservation equation as v = M + 4 M = M + M 4 1 . Using A.M.-G.M. inequality, we get the maximum value of v as v m a x = V = 4 1 when M = M 4 or M = 4 . Hence V × M = 4 1 × 4 = 1 .