Optimum Tapping
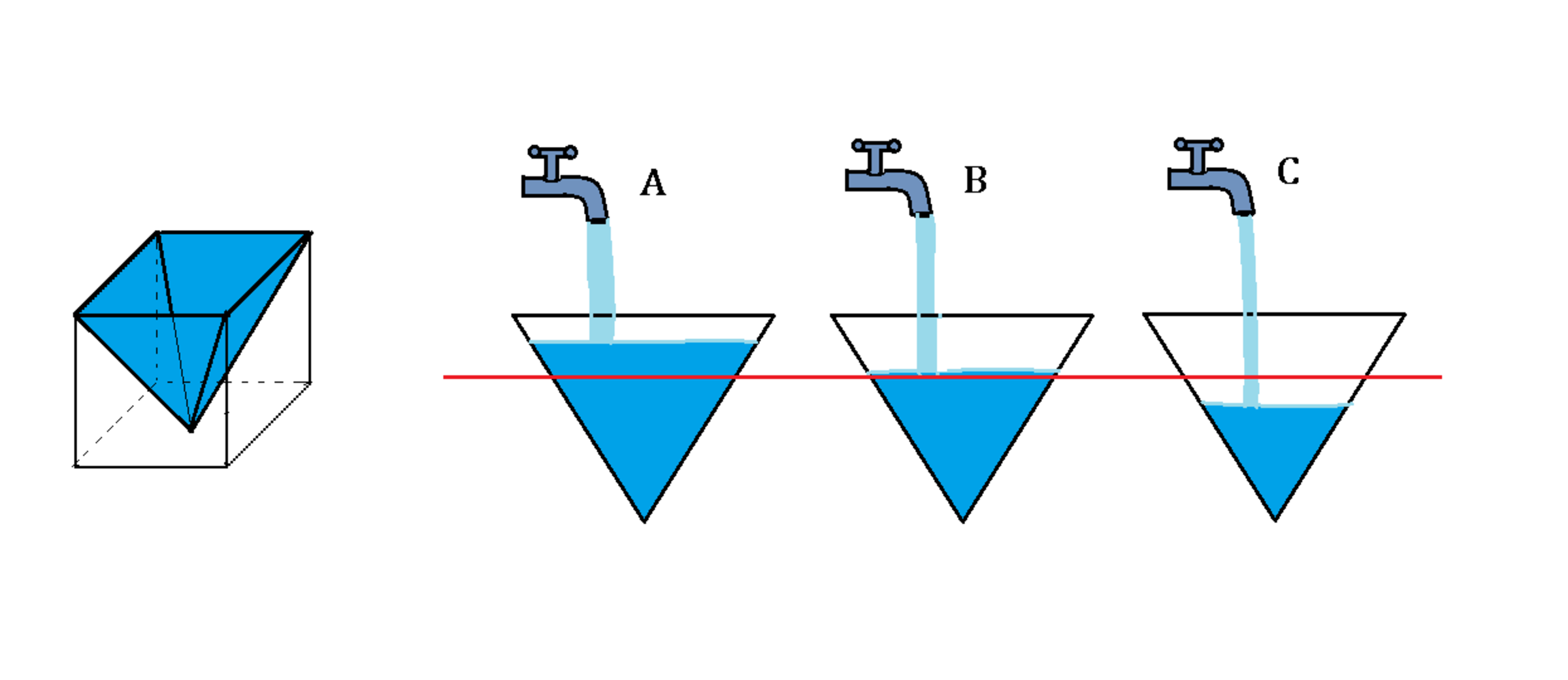
You are filling the water into empty inverted pyramids enclosed within a cube by opening the taps at the same time as shown above.
The tap can release constant water rate of mL/min., and the tap has constant rate of mL/min. However, after a certain time, the pyramid below tap will have a water height cm. higher than the expected one while for tap , the level is cm. lower. Only the pyramid filled with tap has the desired volume.
At that instant, if the rate of change in height for pyramid is times higher than that of pyramid , what is the constant rate of water flow (in mL/min.) for tap ?
The answer is 625.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Suppose the filled pyramid has a height of x . Since it's a pyramid has a square base and is constructed within a cube, its volume will equal 3 x 3 due to triangular similarity.
Now we can set up the equation for rates of change:
d t d v = d h d v ⋅ d t d h
We can evaluate d h d v = d h d 3 x 3 = x 2 .
For tap A , the rate of change at h = x + 1 equals: d t d v = 1 0 8 0 = ( x + 1 ) 2 ⋅ d t d h a .
For tap C , the rate of change at h = x − 1 equals: d t d v = 3 2 0 = ( x − 1 ) 2 ⋅ d t d h c .
The d t d h for tap A is 1 . 5 times of that for tap C .
Hence, when we divide the first equation with the second one, we will get:
3 2 0 1 0 8 0 = ( x − 1 ) 2 ( x + 1 ) 2 ⋅ 1 . 5
4 9 = ( x − 1 ) 2 ( x + 1 ) 2
2 3 = x − 1 x + 1
3 x − 3 = 2 x + 2
x = 5
Now all we need to know is the time T taken to obtain such volume V , and since the rate of change is constant, we can calculate for tap A :
d t d v = T V = 1 0 8 0
1 0 8 0 = 3 T 6 3
T = 1 0 8 0 7 2 = 1 5 1
Finally, we can calculate the flow rate for tap B :
d t d v = T V = 1 5 ⋅ 3 1 ⋅ 5 3 = 6 2 5
Therefore, the tap B has constant flow rate of 6 2 5 mL/min.