Optionnal differences of squares.
How many ways can you make the equation true such that x and y are positive integers?
| x 2 − y 2 = 2 0 1 6 |
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
You have a typo in Method 1: "Subtract one for each number that is a multiple of 4, but not of 2. Else, add one" should be "for each number that is a multiple of 2, but not of 4".
It would also be good for Method 2 to clarify that "On each exponent, subtract one for 2" you mean to subtract one from the exponent of the base 2, not if the exponent is 2. As you show in your table 2^5 => exponent of base 2 is 5 => subtract one from exponent => 5-1 = 4. Before seeing the table, I interpreted it as "3^2 => exponent of base 3 is 2 => subtract one from exponent => 2-1 = 1.
Mateo, the biggest pain consists finding all the divisors, but here https://www2.math.upenn.edu/~deturck/m170/wk2/numdivisors.html there is a way to find them more easily
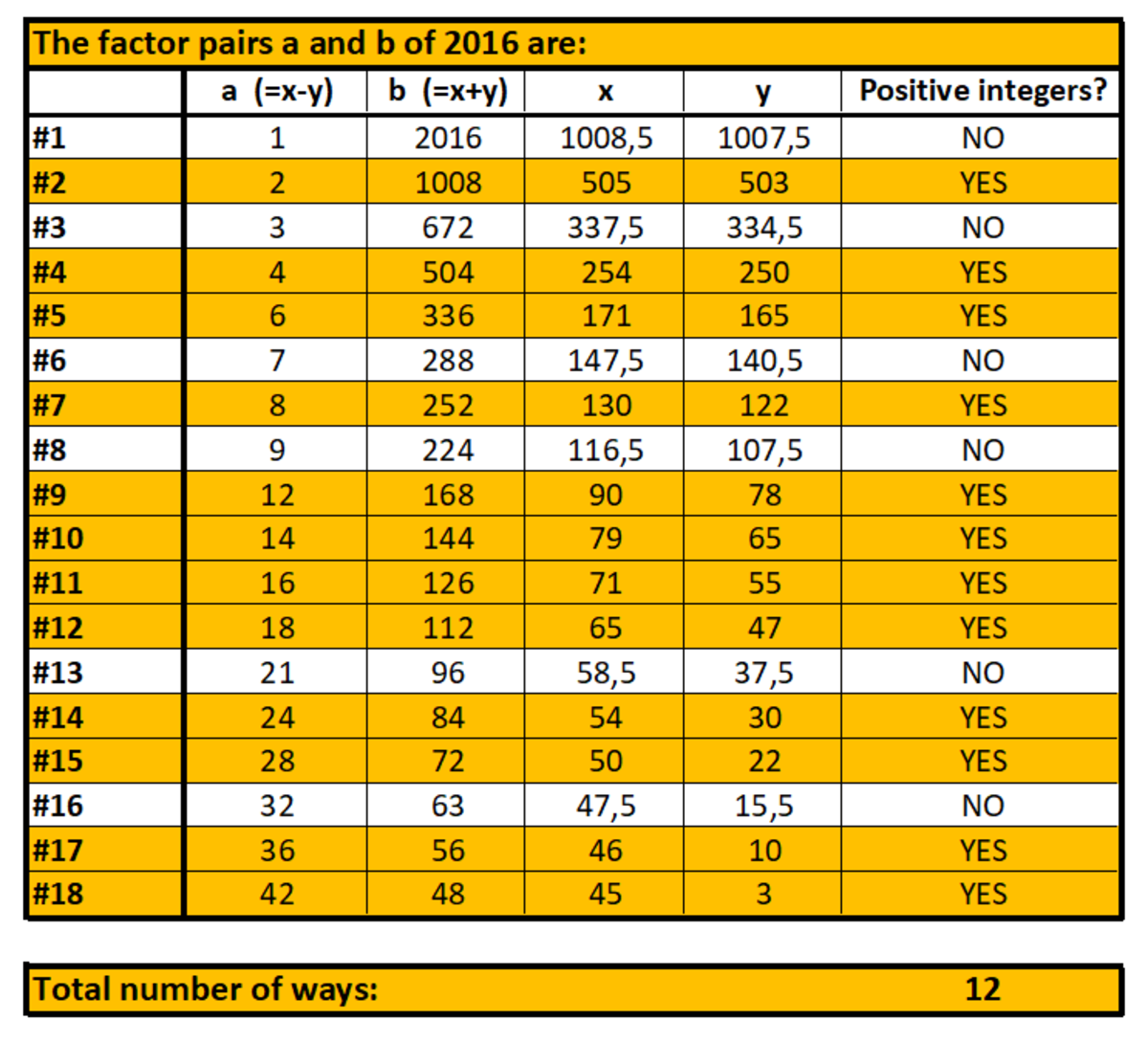
Let's N to be the number of ways we can get positive integer solutions for x 2 − y 2 = 2 0 1 6 , n to be the number of divisors of 2016 and n o the number of odd divisors of 2016, so since 2 0 1 6 = 2 5 × 3 2 × 7 1 ⇒ n = ( 5 + 1 ) × ( 2 + 1 ) × ( 1 + 1 ) = 3 6 .
Now we have to disregard the odd divisors d o i and their complements c o i such that d o i × c o i = 2 0 1 6 . The odd divisors of 2016 are 1, 3, 9, 7, 21 and 63, so n o = 6 . Therefore, N = 2 n − 2 n o = 2 3 6 − 2 × 6 = 1 2
 (
F
a
c
t
o
r
.
p
a
i
r
s
.
f
o
u
n
d
.
u
s
i
n
g
.
h
t
t
p
s
:
/
/
w
w
w
.
c
a
l
c
u
l
a
t
o
r
s
o
u
p
.
c
o
m
/
c
a
l
c
u
l
a
t
o
r
s
/
m
a
t
h
/
f
a
c
t
o
r
s
.
p
h
p
)
(
F
a
c
t
o
r
.
p
a
i
r
s
.
f
o
u
n
d
.
u
s
i
n
g
.
h
t
t
p
s
:
/
/
w
w
w
.
c
a
l
c
u
l
a
t
o
r
s
o
u
p
.
c
o
m
/
c
a
l
c
u
l
a
t
o
r
s
/
m
a
t
h
/
f
a
c
t
o
r
s
.
p
h
p
)
Let's N to be the number of ways we can get positive integer solutions for x 2 − y 2 = ( x + y ) × ( x − y ) = 2 0 1 6 , n to be the number of divisors of 2016 and n o the number of odd divisors of 2016, so since 2 0 1 6 = 2 5 × 3 2 × 7 1 ⇒ n = ( 5 + 1 ) × ( 2 + 1 ) × ( 1 + 1 ) = 3 6 .
Now we have to disregard the odd divisors d o i and their complements c o i such that d o i × c o i = 2 0 1 6 , since both (x - y) and (x + y) must be even. The odd divisors of 2016 are 1, 3, 9, 7, 21 and 63, so n o = 6 . Therefore, N = 2 n − 2 n o = 2 3 6 − 2 × 6 = 1 2
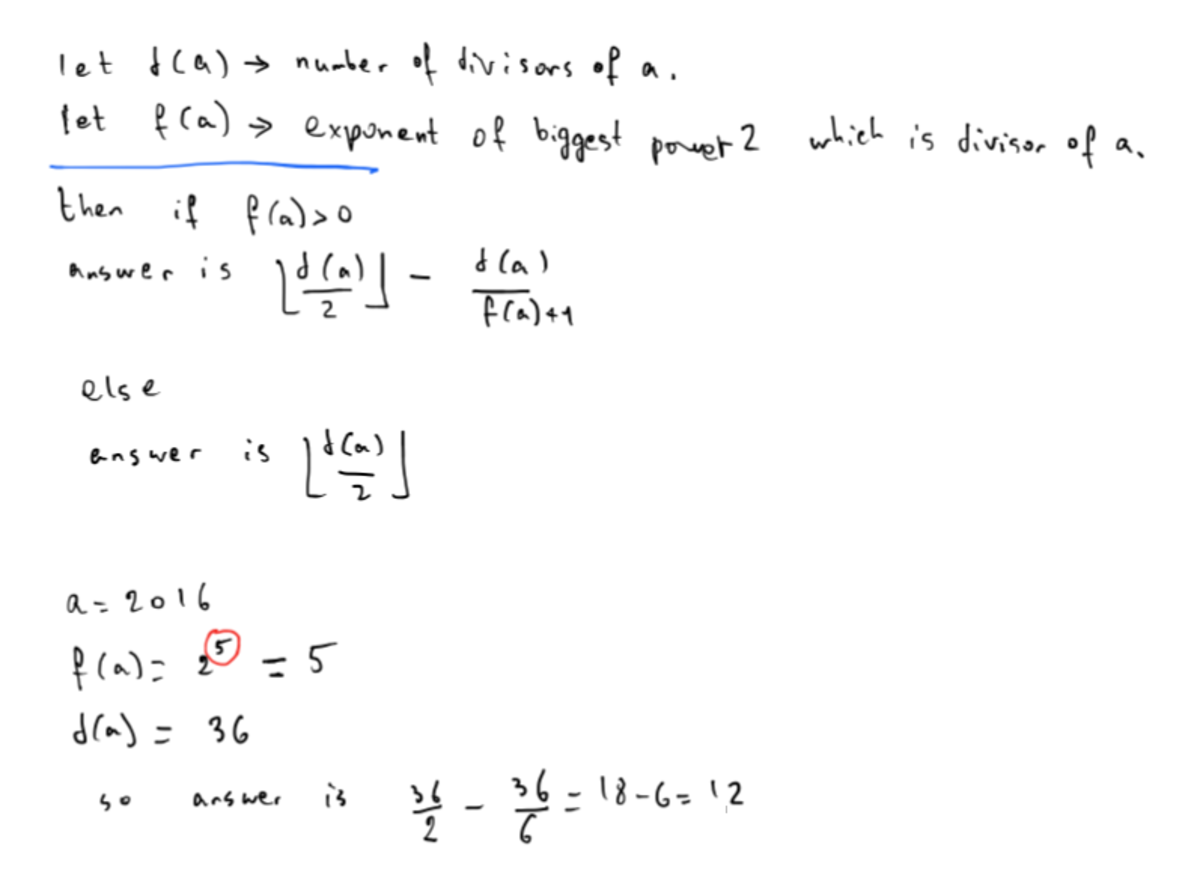
Method 1: all factors
Factors of 2016:
Subtract one for each number that is a multiple of 2, but not of 4 (2, 6, 10, 14...). For all other numbers, add one.
Total: 24
Options: total / 2 = 1 2 solutions
Methed 2: prime numbers (recommended)
Define 2016 by its prime factors. Subtract one from the exponent of the base 2 and add one for the exponent of each of the other bases. Take each of the changed exponents and do the product between these numbers.
Options: total / 2 = 1 2 solutions
Proof
These products all equals 2016. Since 2016 is an even number, each have to be even as well.
Each product can be turned into differences of squares knowing that p × q = ( 2 p + q ) 2 − ( 2 p − q ) 2 ( p ≥ q ) since ( a + b ) ( a − b ) = a 2 − b 2