Origami Angle Challenge

Geometry Level 3

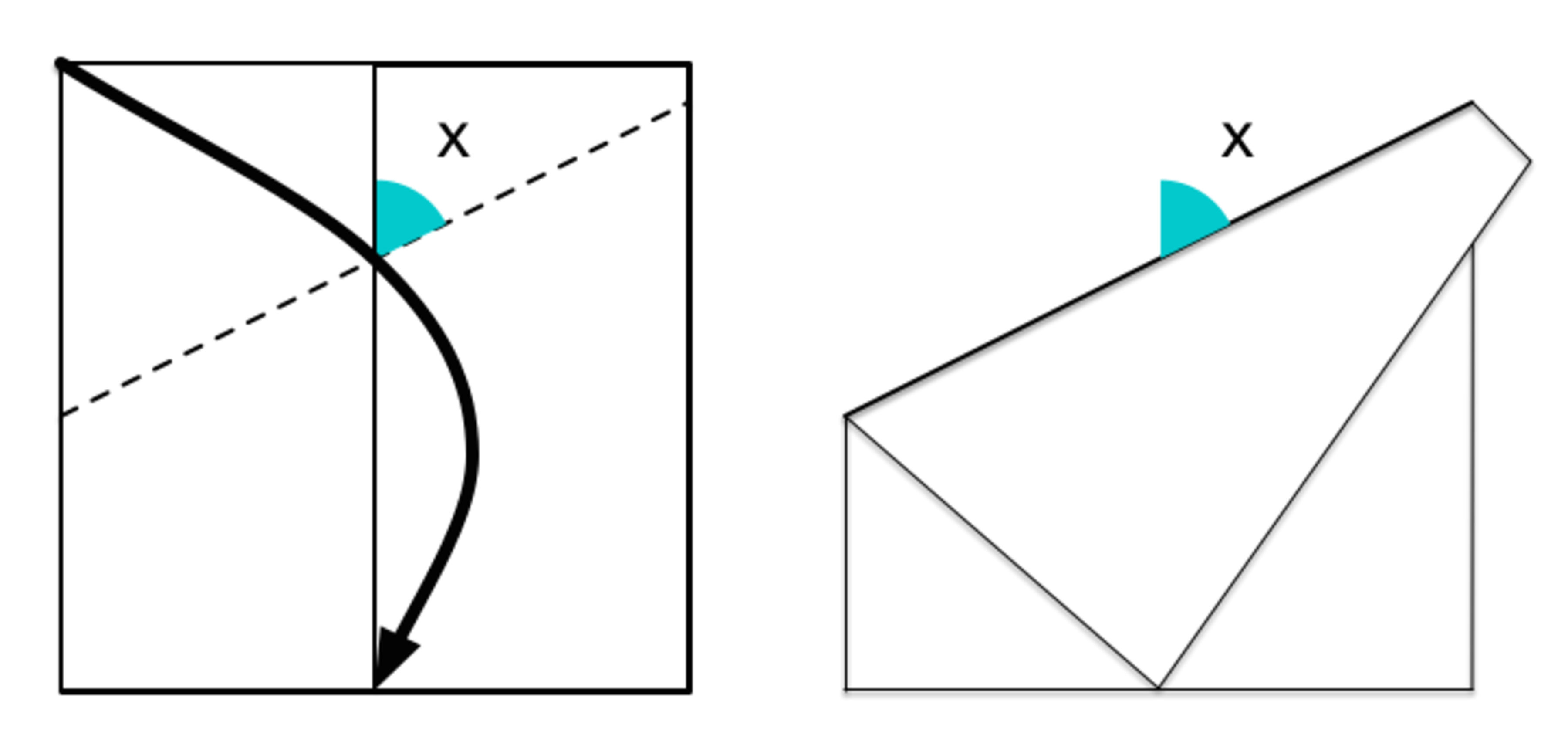
While constructing origami from a square piece of paper, you see an instruction to fold the top left corner onto the bottom midpoint. To the nearest degree, what is the measure of angle $x$ ?

The answer is 63.

2 solutions

Antonio Torrecillas
Mar 5, 2016

The two angles are equal (both lines are perpendicular to DE)

(angle) = arctan(2)= 63.4349º

That's a great observation! The key is that DE is perpendicular to the fold, and we know what the slope of DE is.

Thanks for sharing!

Calvin Lin Staff - 5 years, 3 months ago

Ahmad Saad
Mar 1, 2016

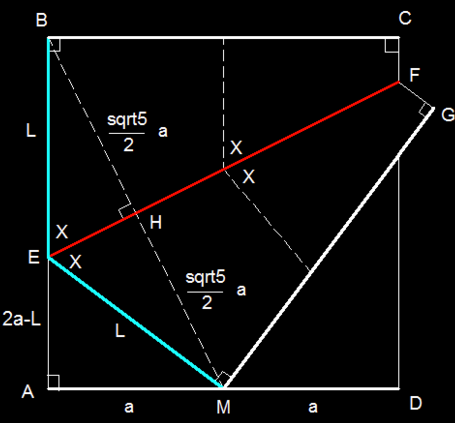
By Pythagorean theorem , for the right triangle $EAM$ , we have

$L^2 = a^2 + (2a- L)^2 \Rightarrow L = \dfrac54 a .$

Similarly, for the right triangle $BAM$ , we have

$(BM)^2 = a^2 + (2a)^2 = 5a ^2 \Rightarrow BM = \sqrt5 a .$

Since $H$ is the midpoint of straight line $BM$ , then $BH = \dfrac12 \cdot BM = a \dfrac{\sqrt5}2$ .

And because we can $BL$ and $BH$ in terms of $a$ , we have $\sin X = \dfrac{BH}{BE} = \dfrac{ a \cdot \sqrt5 /2}{5a/4} = \dfrac{2\sqrt5}5 \Rightarrow X \approx 63.4349^\circ .$

Hence our answer is $\boxed{63}$ .

Origami Angle Challenge

The answer is 63.

2 solutions

0 pending reports