Origami Fun 2
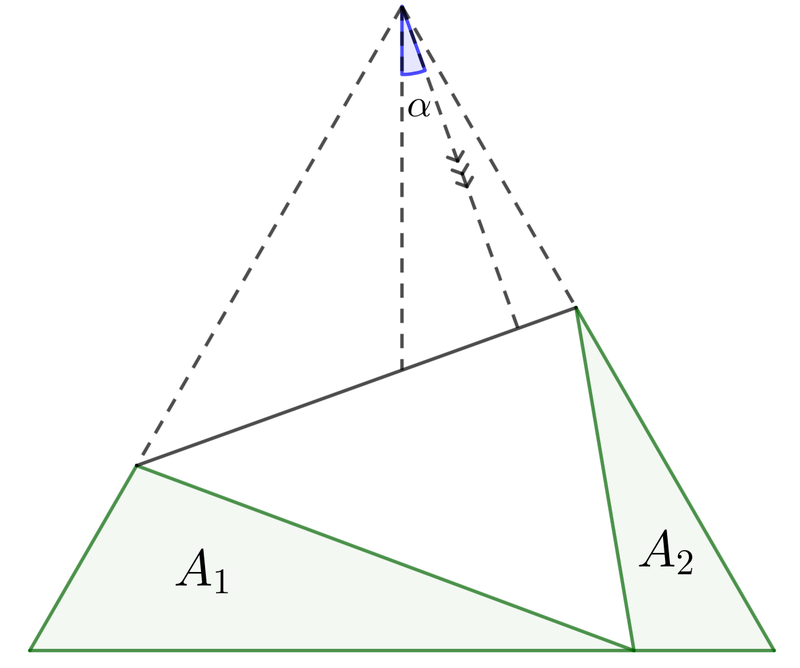
The tip of an equilateral triangular paper is folded at an angle α about an altitude, so that:
- It touches the bottom edge of the paper
- A 1 + A 2 is the area of the resulting folded triangle
If the angle is α in radians, evaluate ⌊ 1 0 5 α ⌋ .
The answer is 34543.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
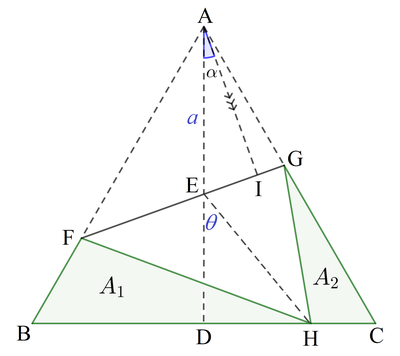
First note that △ A F G and △ F G H are congruent. Then 3 ( A 1 + A 2 ) = A △ , where A △ is the area of △ A B C . Let the side length of the equilateral triangular paper be 2 . Then A △ = 2 2 2 sin 6 0 ∘ = 3 and A 1 + A 2 = 3 1 .
Since A B = B C = C A = 2 , A D = 3 . Let A E = a , then E H = A E = a and E D = 3 − a . Let ∠ D E H = θ . Then ∠ A E G = 2 1 ∠ A E H = 9 0 ∘ − 2 θ . Since ∠ A E G = 9 0 ∘ − α also, then θ = 2 α and cos 2 α = E H E D = a 3 − a .
Note that ∠ A G E = 6 0 ∘ + α and ∠ A F E = 6 0 ∘ − α . By sine rule , sin 3 0 ∘ E F = sin ( 6 0 ∘ − α ) a and sin 3 0 ∘ E G = sin ( 6 0 ∘ + α ) a . And the area [ F G H ] = [ A F G ] is given by:
[ A F G ] A 1 + A 2 3 1 8 cos 3 α ( cos 2 α − cos 1 2 0 ∘ ) 4 ( cos 2 α + 1 ) ( cos 2 α + 2 1 ) 2 ( cos 2 α + 1 ) ( 2 cos 2 α + 1 ) 4 cos 2 2 α + 6 cos 2 α − 7 ⟹ cos 2 α α ⟹ ⌊ 1 0 5 α ⌋ = 2 A I ⋅ F G = 2 a cos α ⋅ ( E F + E G ) = 4 a 2 cos α ( sin ( 6 0 ∘ − α ) 1 + sin ( 6 0 ∘ + α ) 1 ) = 1 6 cos 3 α sin ( 6 0 ∘ + α ) sin ( 6 0 ∘ − α ) 3 ( sin ( 6 0 ∘ + α ) + sin ( 6 0 ∘ − α ) ) = 9 cos α = 9 = 9 = 0 = 4 3 7 − 3 ≈ 0 . 3 4 5 4 3 6 0 2 3 = 3 4 5 4 3 As cos 2 α = a 3 − a
Let the sides of the equilateral triangle be 1 and label the diagram as follows:
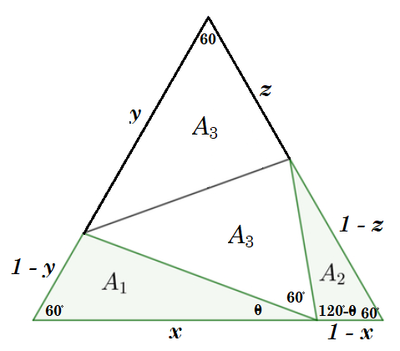
From the area of the equilateral triangle, A 1 + A 2 + 2 A 3 = 2 1 ⋅ 1 ⋅ 1 ⋅ sin 6 0 ° = 4 3 , and from the given information, A 1 + A 2 = A 3 . Combining these equations gives A 3 = 1 2 3 .
Also,
A 1 = 2 1 ⋅ x ⋅ ( 1 − y ) ⋅ sin 6 0 ° = 4 3 x ( 1 − y )
A 2 = 2 1 ⋅ ( 1 − x ) ⋅ ( 1 − z ) ⋅ sin 6 0 ° = 4 3 x ( 1 − x ) ( 1 − z )
A 3 = 2 1 ⋅ y ⋅ z ⋅ sin 6 0 ° = 4 3 y z = 1 2 3
Since A 1 + A 2 = A 3 , 4 3 x ( 1 − y ) + 4 3 x ( 1 − x ) ( 1 − z ) = 4 3 y z = 1 2 3 , or after simplifying,
3 x ( 1 − y ) + 3 ( 1 − x ) ( 1 − z ) = 1
3 y z = 1
By the law of sines on A 1 , 1 − y sin θ = y sin 6 0 ° , and if s = sin θ , this simplifies to:
2 s y = 3 ( 1 − y )
By the law of sines on A 2 , 1 − z sin ( 1 2 0 ° − θ ) = z sin 6 0 ° , and since sin ( 1 2 0 ° − θ ) = sin 1 2 0 ° cos θ − cos 1 2 0 ° sin θ = 2 1 ( 3 cos θ + sin θ ) = 2 1 ( 3 ( 1 − sin 2 θ ) + sin θ ) , if s = sin θ this simplifies to:
z 3 ( 1 − s 2 ) + s z = ( 1 − z ) 3
The four equations solve numerically to s ≈ 0 . 3 4 8 8 3 3 , x ≈ 0 . 8 1 1 6 5 2 , y ≈ 0 . 7 1 2 8 6 1 , and z ≈ 0 . 4 6 7 5 9 9 .
Now applying some trigonometry to △ P Q R that is labeled below:
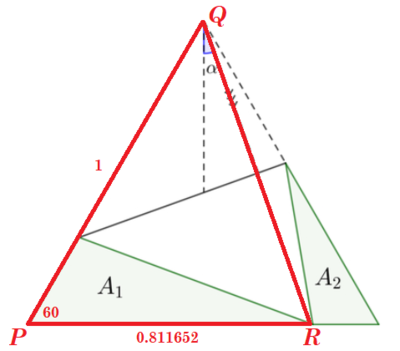
By the law of cosines, Q R = P Q 2 + P R 2 − 2 ⋅ P Q ⋅ P R ⋅ cos 6 0 ° ≈ 1 2 + 0 . 8 1 1 6 5 2 2 − 2 ⋅ 1 ⋅ 0 . 8 1 1 6 5 2 ⋅ 2 1 ≈ 0 . 9 2 0 3 9 5 .
And also by the law of cosines, P R = P Q 2 + Q R 2 − 2 ⋅ P Q ⋅ Q R ⋅ cos ∠ Q , or 0 . 8 1 1 6 5 2 ≈ 1 2 + 0 . 9 2 0 3 9 5 2 − 2 ⋅ 1 ⋅ 0 . 9 2 0 3 9 5 ⋅ cos ( 3 0 ° + α ) , which solves to α ≈ 0 . 3 4 5 4 3 6 .
Therefore, ⌊ 1 0 5 α ⌋ = ⌊ 1 0 5 ⋅ 0 . 3 4 5 4 3 6 ⌋ = 3 4 5 4 3 .
Moreover, [ A D E ] = [ F D E ] = A 1 + A 2 and [ A D E ] + [ F D E ] + A 1 + A 2 = [ A B C ] thus, [ A D E ] = 3 1 [ A B C ] Let △ A B C be of unit side length and denote A H by x .
Then, on △ A M F ,
A F = cos a A M ⇒ 2 x = cos a 2 3 ⇒ x 2 = 1 6 3 ⋅ cos 2 a 1 ⇒ x 2 = 1 6 3 ⋅ ( 1 + tan 2 a ) Consequently,
[ A D E ] 2 1 D E ⋅ A H ( D H + H E ) ⋅ A H ( x tan ( 6 π + a ) + x tan ( 6 π − a ) ) ⋅ x x 2 ( 1 − tan 6 π ⋅ tan a tan 6 π + tan a + 1 + tan 6 π ⋅ tan a tan 6 π − tan a ) 1 6 3 ( 1 + tan 2 a ) ( 2 ⋅ 1 − 3 1 ⋅ tan 2 a 1 + tan 2 a ) = 3 1 ⋅ 4 3 = 1 2 3 = 6 3 = 6 3 = 6 3 = 6 3 ( 1 ) Setting y = tan 2 a , ( 1 ) ⇔ 1 6 3 ( 1 + y ) ( 2 ⋅ 1 − 3 1 y 1 + y ) = 6 3 which simplifies to 9 y 2 + 2 2 y − 3 = 0 Since y > 0 we get y = 9 2 3 7 − 1 1 Thus, tan a = 3 2 3 7 − 1 1 ⇒ a = tan − 1 ( 3 2 3 7 − 1 1 ) ≈ 0 . 3 4 5 4 3 6 0 2 2 6 For the answer, ⌊ 1 0 5 a ⌋ = 3 4 5 4 3 .