Origami Fun
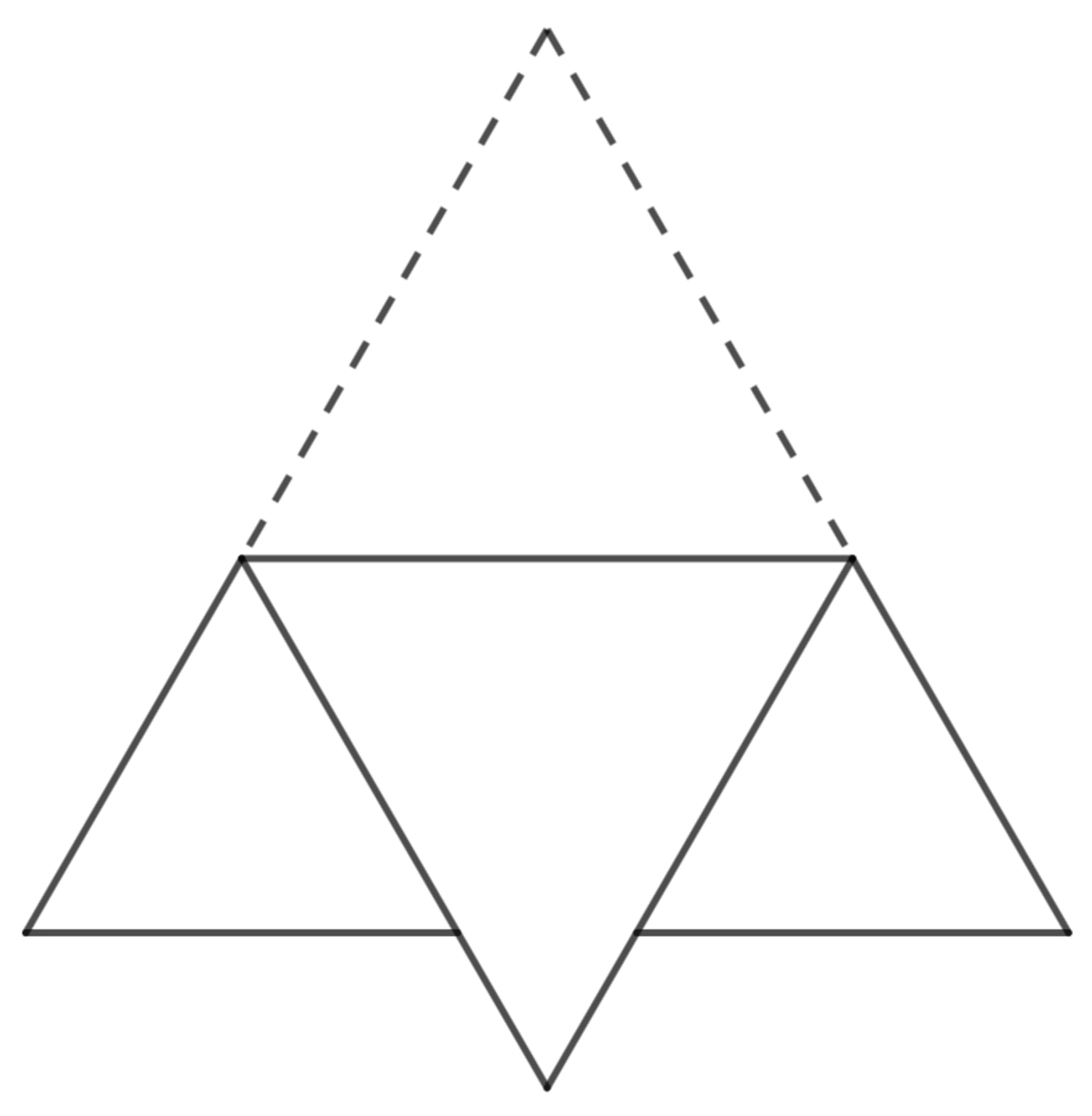
The top tip of an equilateral triangular paper of a unit side length is folded orthogonally toward the bottom segment, so that the area of the folded triangle is twice the area of either of the small triangles. If the side length of the folded triangle is s 1 , and the side length of the small triangle is s 2 , evaluate ⌊ 1 0 0 0 ( s 1 + 2 s 2 ) ⌋ .
The answer is 1414.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Note that s 1 + s 2 = 1 , the side length of the equilateral triangular paper. For figure of the same shape, in this case the equilateral triangle, area is directly proportional to the square of the linear dimension, in this case the side length. This means that s 2 2 s 1 2 = 2 ⟹ s 1 = 2 s 2 . Then we have:
s 1 + s 2 ( 2 + 1 ) s 2 ⟹ s 2 s 1 + 2 s 2 ⟹ ⌊ 1 0 0 0 ( s 1 + 2 s 2 ) ⌋ = 1 = 1 = 2 + 1 1 = ( 2 + 2 ) s 2 = 2 + 1 2 + 2 = 2 + 1 2 ( 2 + 1 ) = 2 = ⌊ 1 0 0 0 2 ⌋ = 1 4 1 4
Since the large triangle has side length 1 and is equilateral, its height is given by sin(60 degrees) = sqrt(3) / 2. Let h be the height of the folded triangle. We then see that the height of the little triangle is sqrt(3)/2 - h. Hence, we have:
Area(folded triangle) = A(fold) = (1/2) h s1, and
Area(little triangle) = A(little) = (1/2) (s2) (sqrt(3)/2 - h) = (1/2) (1-s1) (sqrt(3)/2 - h)
(the last equality follows since s1 + s2 = 1 = length of the side of the big triangle).
Utilizing the relationship A(fold) = 2*A(little) we find:
(1/2) (s1) h = (1-s1)*(sqrt(3)/2 - h) (equation 1)
But, from the folded triangle, we find:
tan(60 degrees) = sqrt(3) = h/((s1)/2), so that:
h = (s1)*sqrt(3)/2
Substituting this into equation 1 and simplifying yields the equation:
(s1)^2 -4*s1 +2 = 0 or
s1 = 2 - sqrt(2) (we reject the negative root).
Hence, s2 = 1-s1 = sqrt(2) - 1, so that
1000 (s1 + 2 s2) = 1000*sqrt(2)
The greatest integer function of this last quantity is 1414.
Note that all triangles in the figure are equilateral triangles. Denote by A 1 , A 2 the areas of the equilateral triangles of side s 1 and s 2 respectively.
Then, we have A 2 A 1 = 2 ⇒ ( s 2 s 1 ) 2 = 2 ⇒ s 1 2 = 2 s 2 2 ⇒ s 1 = s 2 2 ( 1 ) Moreover,
s 1 + s 2 = 1 ⇒ ( 1 ) s 2 2 + s 2 = 1 ⇒ s 2 ( 2 + 1 ) = 1 ⇒ s 2 = 2 + 1 1 ⇒ s 2 = 2 − 1 Hence, ( 1 ) ⇒ s 1 = ( 2 − 1 ) 2 ⇒ s 1 = 2 − 2 Finally,
s 1 + 2 s 2 = 2 − 2 + 2 ( 2 − 1 ) = 2 ≈ 1 , 4 1 4 3 For the answer, ⌊ 1 0 0 0 ( ( s 1 + 2 s 2 ) ) ⌋ = 1 4 1 4 .