Origami in the 3D space
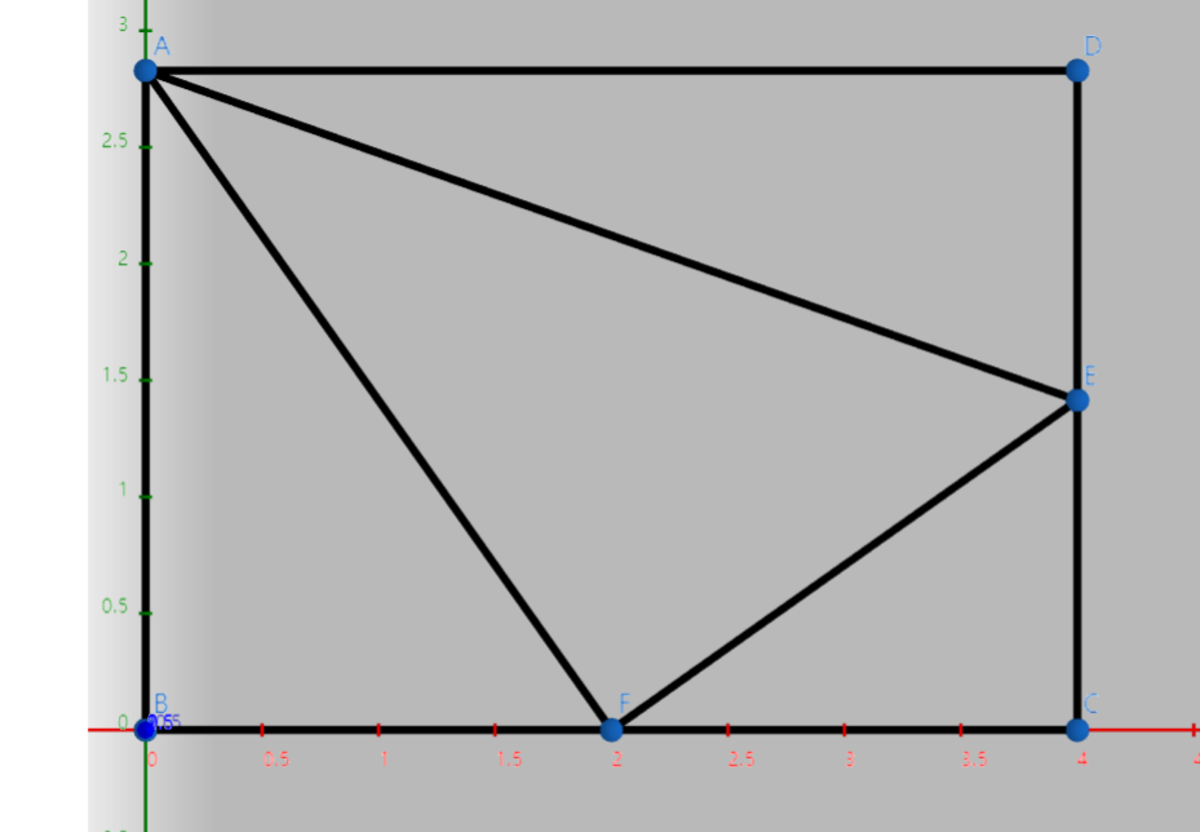 Above is the rectangle
, where
, and
are the midpoints of
respectively.
Above is the rectangle
, where
, and
are the midpoints of
respectively.
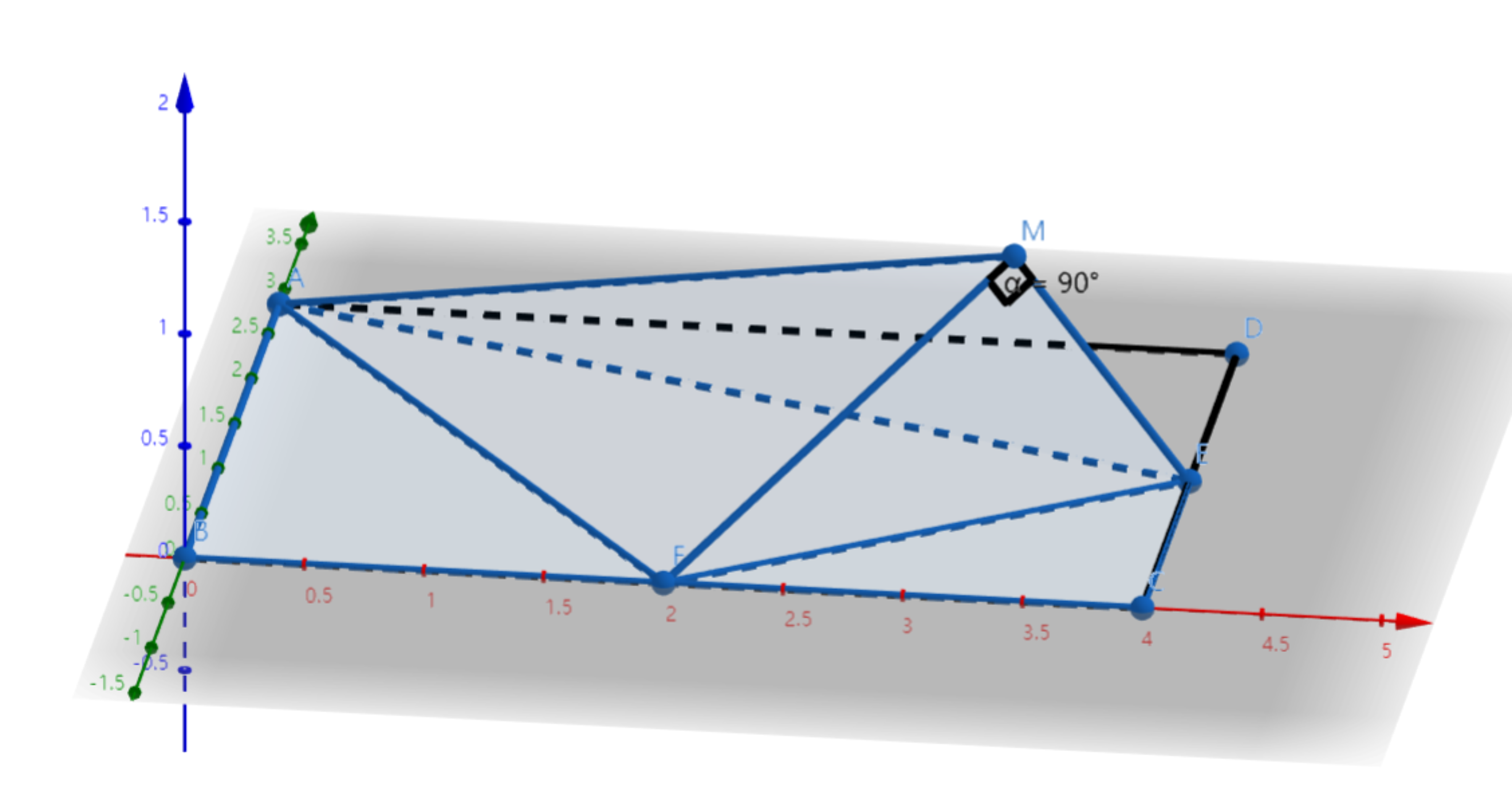
If we fold along in the 3D space to so that , as shown above, then find the dihedral angle . Submit the angle in degrees and round to the hundredth.
The answer is 60.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the coordinates of M be ( x , y , z ) . Then by the distance formula, M E = 2 = ( x − 4 ) 2 + ( y − 2 ) 2 + z 2 , M F = 2 = ( x − 2 ) 2 + y 2 + z 2 , and M A = 4 = x 2 + ( y − 2 2 ) 2 + z 2 , which solves to M ( x , y , z ) = M ( 3 1 0 , 3 2 2 , 3 2 3 ) for z > 0 .
The equation of the plane with A , E , and M can be expressed generally as x + b y + c z = d . A ( 0 , 2 2 , 0 ) gives 2 2 b = d , E ( 4 , 2 , 0 ) gives 4 + 2 b = d and M ( 3 1 0 , 3 2 2 , 3 2 3 ) gives 3 1 0 + 3 2 2 b + 3 2 3 c = d , which solves to x + 2 2 y + 3 z = 8 .
The equation of the plane with A , E , and F is z = 0 .
The normal to x + 2 2 y + 3 z = 8 is ( 1 , 2 2 , 3 ) and the normal to z = 0 is ( 0 , 0 , 1 ) . The angle θ between these normals (and also the dihedral angle between the two planes) is θ = cos − 1 ( 1 2 + ( 2 2 ) 2 + ( 3 ) 2 ⋅ 0 2 + 0 2 + 1 2 ( 1 , 2 2 , 3 ) ⋅ ( 0 , 0 , 1 ) ) = cos − 1 ( 2 1 ) = 6 0 ° .