Origami Triangle
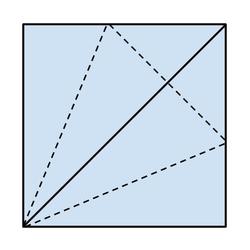 I have a piece of square paper, which I fold in half diagonally and crease. Flattening the paper out again, I fold over one side so that the side lines up with this crease. I repeat this with the adjacent side, making a symmetrical kite shape. I then fold the triangle of remaining 'upwards' facing paper down to form one larger triangle. What is the area of this triangle divided by the area of the original square?
I have a piece of square paper, which I fold in half diagonally and crease. Flattening the paper out again, I fold over one side so that the side lines up with this crease. I repeat this with the adjacent side, making a symmetrical kite shape. I then fold the triangle of remaining 'upwards' facing paper down to form one larger triangle. What is the area of this triangle divided by the area of the original square?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Good work!
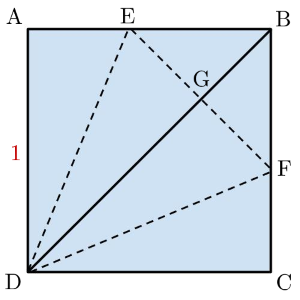
Let [ △ X Y Z ] denote the area of △ X Y Z .
From the picture we note that ∠ A D B = 4 5 ° and due to similar triangles, ∠ A D E = ∠ E D G = 2 2 . 5 ° .
Thus the length of A E is tan 2 2 . 5 ° and [ △ A E D ] = 2 tan 2 2 . 5 ° , [ △ D E F ] = tan 2 2 . 5 ° . Therefore the area of the △ D E F divided by the area of the square ( 1 ) is tan 2 2 . 5 ° .
To work out the exact value of tan 2 2 . 5 ° we can start by recalling that tan 4 5 ° = 1 . Therefore we are trying to find x where tan 2 x = 1 . Let y = tan x , and via the tan ( A + B ) rule we have:
1 − y 2 2 y = 1 ⇒ y 2 + 2 y − 1 = 0
Putting this into the quadratic formula gives y = − 1 ± 2 . Obviously our answer must be positive so we have [ △ D E F ] = 2 − 1 .
Let the square's side length be 1. The square's area will also be 1, so the area of the triangle divided by the area of the square is equal to the area of the triangle in this case. We know the height of the triangle in question is 1, since it is determined by folding over a side of the square. The height of the little triangle (in the top right) is the length of the diagonal subtracted by the height of the big triangle, which is 2 − 1 . Imagine this little triangle split into two smaller triangles by the diagonal line. These are isosceles triangles, with angles 90/45/45. Thus, the length of the base of our big triangle is 2 ( 2 − 1 ) . The area of the large triangle is 2 1 ∗ 2 ( 2 − 1 ) ∗ 1 ( 2 1 ∗ b a s e ∗ h e i g h t ), so the area of the triangle divided by the area of the square is 2 − 1 .
Label the diagram as shown. The area of the square is equal to x 2 . From the picture it is clear that length DG is x (it's AD folded over). By Pythagoras' theorem, Length DB is x 2 + x 2 , that is 2 x . Hence, length GB is 2 x − x . Triangle BGF is isoceles, so GF is also 2 x − x . EF is double this, that is 2 ( 2 x − x ) . Hence, the area of triangle DEF is 0 . 5 × 2 ( 2 x − x ) × x (from 0 . 5 × b a s e × h e i g h t ) . When we divide this by x 2 , we get x 2 x ( 2 x − x ) . Finally, by cancelling x, the area is 2 − 1 .