Origin Story
Neutrinos arrive at Earth's surface all the time. Energies below ∼ 5 0 G eV are typical and result from the breakdown of other particles high in the atmosphere. But last fall, a neutrino arrived with an energy of 2 9 0 T eV , about 2 0 times more energetic than the most powerful collisions at the LHC. At the moment, our understanding of where these exceptional particles could come from is poor.
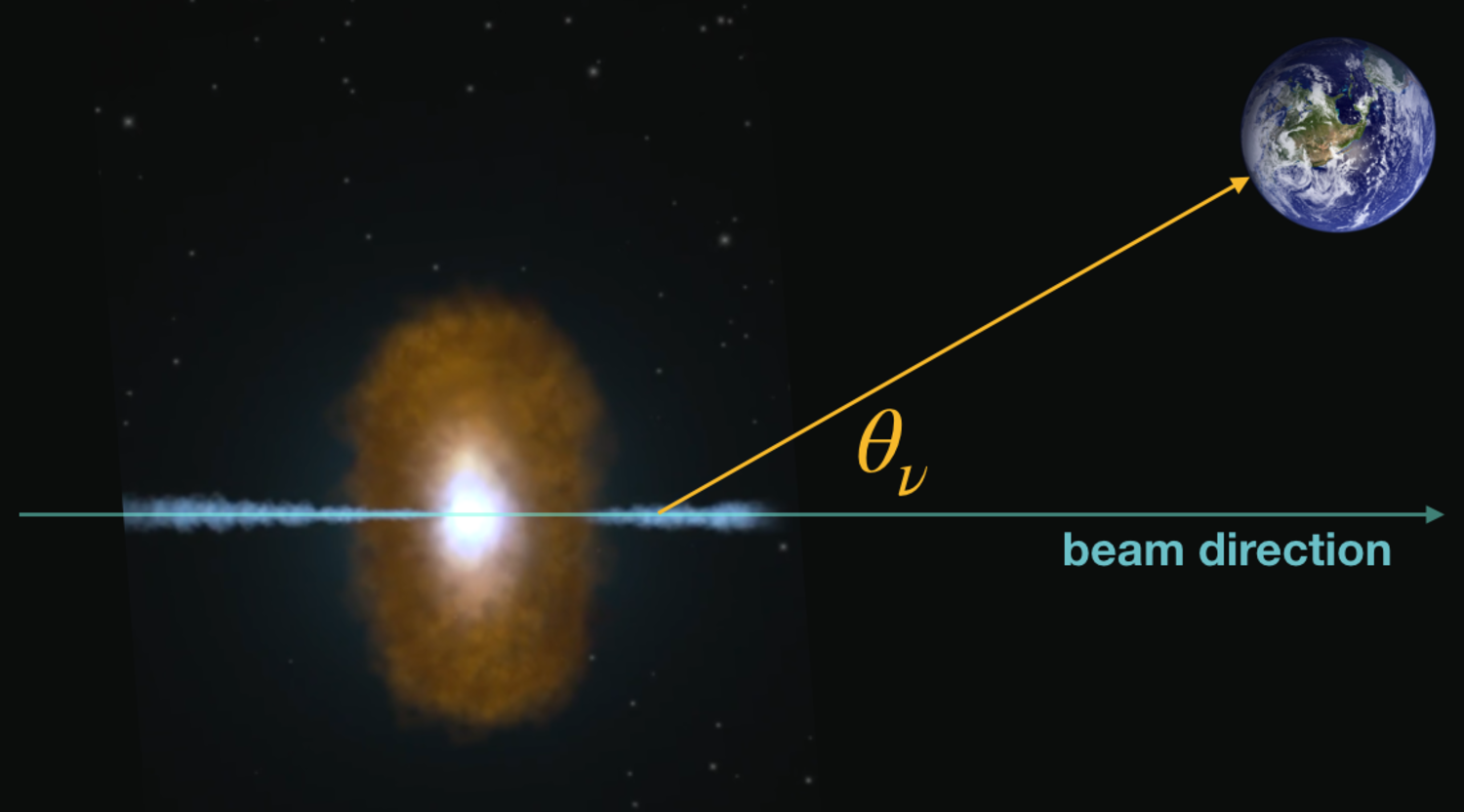
Evidence is pointing toward a blazar in the direction of constellation Orion, which comprises a galaxy that orbits a spinning, supermassive black hole (SMBH). Calculations suggest that such SMBH form powerful jets that eject matter along their axis of rotation. The idea is that a very high energy pion π − was accelerated in the jet before decaying into a neutrino ν μ and a muon μ − , and that the neutrino sailed billions of years across the Universe, before landing at the IceCube detector in Antarctica.
Suppose a neutrino with energy E ν is produced by a charged-pion decay process (which also produces a muon): π − → μ − + ν μ .
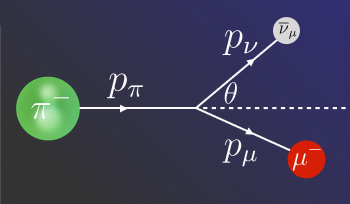
Use conservation of momentum and conservation of energy to calculate the pion's energy E π at the maximum possible angle θ that sent the 2 9 0 T eV neutrino hurtling at Antarctica.
How many times larger is E π compared to E ν ?
Note: At ultra-high energies, the relationship between a particle's energy E and momentum p is E = p 2 c 2 + m 2 c 4 , where m is the particle's mass ( instead of the classical relationship E = p 2 / 2 m ) .
Assume the pion's mass m π = 1 4 0 M eV / c 2 and the muon's mass m μ = 1 0 6 M eV / c 2 . The neutrino's mass is so small that you can assume it is 0 .
The answer is 4.68675.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
If P π , P ν , P μ are the 4 -momenta of the pion, neutrino and muon respectively, then P π = P ν + P μ . In a suitably oriented rest-frame of the pion, we will have P π = ( m π c , 0 , 0 , 0 ) , P ν = ( p , p , 0 , 0 ) and P μ = ( c − 1 E μ , − p , 0 , 0 ) where m π c = p + c − 1 E μ . But this means that m π c 2 − p c ( m π c 2 − p c ) 2 p = E μ = p 2 c 2 + m μ 2 c 4 = p 2 c 2 + m μ 2 c 4 = 2 m π ( m π 2 − m μ 2 ) c and hence p c ≈ 2 9 . 8 7 1 1 4 3 M e V .
Now suppose we are in a laboratory frame, where the pion is moving along the x -axis with speed v . In the matching rest frame of the pion, we have P ν = ( p , p cos α , p sin α , 0 ) for some angle α , and so the 4 -momentum of the neutrino in the laboratory frame is P ν = γ p ( 1 + c v cos α , cos α + c v , sin α , 0 ) = c − 1 E ν ( 1 , cos θ , sin θ , 0 ) where E ν = 2 7 0 T e V and θ is the deflection angle. Here γ = ( 1 − c 2 v 2 ) − 2 1 .
Write w = c v . Then γ = ( 1 − w 2 ) − 2 1 . We require γ p c ( 1 + w cos α ) cos α = E ν = w − 1 ( γ K − 1 ) where K = p c E ν ≈ 9 . 7 0 8 3 7 × 1 0 6 . For this to be possible, we must have − 1 ≤ cos α ≤ 1 , and for this to be true we require that K 2 + 1 K 2 − 1 ≤ w < 1 o r γ ≥ 2 K K 2 + 1 In other words, the pion has to be highly energetic. But this means that cos θ = 1 + w cos α cos α + w = K γ w K γ − 1 = K w K − 1 − w 2 and the smaller cos θ gets, the larger the displacement angle becomes. Now d w d cos θ = W w 2 1 − w 2 1 − K 1 − w 2 and this vanishes when γ = K . The maximum displacement angle occurs when v is such that γ = K .
In the laboratory rest frame P π = ( γ m π c , γ m π v , 0 , 0 ) , and hence E π = γ m π c 2 = K m π c 2 , and so E ν E π = K p c K m π c 2 = p c 1 4 0 = m π 2 − m μ 2 2 m π 2 = 4 . 6 8 6 7 5 2 7 5
Without claiming that every step is rigorous, I offer this intuitive argument:
- Given that the mass of the π − is so small relative to its kinetic energy, we expect θ to be small, certainly less than π / 2 .
- The maximum ejection angle is achieved when the pion decays perpendicular to the beam direction, in the rest frame of the pion. Ejecting along any other direction would boost p ν x relative to p ν y , lowering θ toward the beam direction. (for simplicity, the beam is the stream of matter that's ejected by the SMBH)
- Because the momentum of the neutrino and muon are perpendicular to the beam direction, their total energy transforms like E ′ = γ E in a frame shift (as does the energy of the pion).
- Because E π , E μ , and E ν all scale by the same factor in a frame shift, we can evaluate the ratio in any frame we like. In other words E π ′ / E ν ′ = E π / E ν .
The easiest frame to evaluate the energies of the pion and the neutrino is in the rest frame of the pion where the neutrino and muon eject vertically, and we have E π = m π c 2 and E ν = p ν y c .
By conservation of energy, we have ( E π − E ν ) 2 ( m π c 2 − p ν y c ) 2 m π 2 c 4 + ( p ν y c ) 2 − 2 m π c 2 p ν y c = E μ 2 = m μ 2 c 4 + ( p μ y c ) 2 = m μ 2 c 4 + ( p μ y c ) 2
By conservation of momentum, p ν y = − p μ y , so we can solve the last equation for p ν y , finding E ν = p ν y c = c 2 2 m π m π 2 − m μ 2 , and therefore E π / E ν = m π 2 − m μ 2 2 m π 2 .
Using my notation, the maximum angle θ occurs when γ = K . Since cos α = 0 in that case, the maximum deflection does indeed occur when the muon and neutrino are emitted normally to the beam direction (in the rest frame of the pion).
Using momentum conservation, the ratio of pion to neutrino energy is:
2(140)^2/{(140-106)+2(140-106)*106} = 4.6867
The pion, before it decays, has energy E π , and its momentum has a magnitude p π . Likewise, the neutrino has energy E ν and momentum p ν , and the muon has energy E μ and momentum p μ .
In special relativity, these quantities have different values in different reference frames, but we will work in the laboratory frame, where the energy of the neutrino is E ν = 2 9 0 T eV . We are looking for E π / E ν starting from the relationships that come about by applying conservation of energy and conservation of momentum.
If we pick the x -axis to be along the trajectory of the pion, then θ is the angle that the neutrino's momentum makes with the x -axis, and α is the angle that the muon's momentum makes with the x -axis. Thus, conservation of momentum gives us two relationships between the momenta:
p π 0 = p ν cos θ + p μ cos α = p ν sin θ + p μ sin α .
We can combine these into a single relationship by eliminating α , the direction of the muon's trajectory:
p μ 2 = p μ 2 cos α 2 + p μ 2 sin α 2 = p ν 2 sin θ 2 + ( p π − p ν cos θ ) 2 = p ν 2 + p π 2 − 2 p π p ν cos θ .
This relationship is satisfied by a range of particle momenta and angles, but not all combinations will satisfy conservation of energy. Since we are only interested in combinations for which energy is conserved, we can use the energy-momentum relationship E 2 = p 2 c 2 + m 2 c 4 to recast this relationship in terms of the particle energies.
For each particle, the energy-momentum relationship can be solved for momentum: p 2 = E 2 / c 2 − m 2 c 2 , and so
p μ 2 c 2 E μ 2 − m μ 2 c 2 E μ 2 = p ν 2 + p π 2 − 2 p π p ν cos θ = c 2 E π 2 − m π 2 c 2 + c 2 E μ 2 − 2 c 2 E π 2 − m π 2 c 2 c E ν cos θ = E ν 2 + E π 2 − ( m π 2 − m μ 2 ) c 4 − 2 E ν E π 2 − m π 2 c 4 cos θ .
In the above result, the mass of the neutrino is set to zero. Now we can impose energy conservation E μ = E π − E ν and find a relationship between the two energies, E ν and E π , we are interested in:
( E π − E ν ) 2 = E ν 2 + E π 2 − ( m π 2 − m μ 2 ) c 4 − 2 E ν E π 2 − m π 2 c 4 cos θ .
Expanding the right-hand side and simplifying, we find the following relationship between the energy of the pion E π and the energy of the neutrino E ν , depending on the angle θ that the neutrino makes relative to the trajectory of the pion:
E π E ν = E ν E π 2 − m π 2 c 4 cos θ + Δ
where we have defined Δ = 2 1 ( m π 2 − m μ 2 ) c 4 .
We're done imposing conservation of momentum and energy, so now all that's left is to solve for the energy of the pion, E π , and determining the largest possible angle of the neutrino's trajectory, θ m .
Moving Δ to the left-hand side, and squaring both sides, we find
( E π E ν − Δ ) 2 E π 2 E ν 2 sin 2 θ − 2 Δ E ν E π + ( Δ 2 + E ν 2 m π 2 c 4 cos 2 θ ) = E ν 2 ( E π 2 − m π c 4 ) cos 2 θ = 0
Using the quadratic formula, we can solve for E π :
E π = 2 E ν 2 sin 2 θ 2 Δ E ν E π ± 2 Δ E ν cos θ 1 − Δ 2 E ν 2 m π 2 c 4 sin 2 θ .
The energy must be real and positive, so we see that Δ 2 E ν 2 m π 2 c 4 sin 2 θ ≤ 1 , and the largest possible angle θ m for which this is true is
sin 2 θ m = m π 2 c 4 E ν 2 Δ 2 .
The expression under the radical is 0 in this case, so
E π = E ν Δ 2 Δ m π 2 c 4 E ν 2 = Δ m π 2 c 4 E ν .
Plugging in the definition of Δ we find
E ν E π = m π 2 − m μ 2 2 m π 2 ,
which works out to E π / E ν = 4 . 6 8 6 7 5 using the measured masses of the pion and muon.