Orthogonal Circles
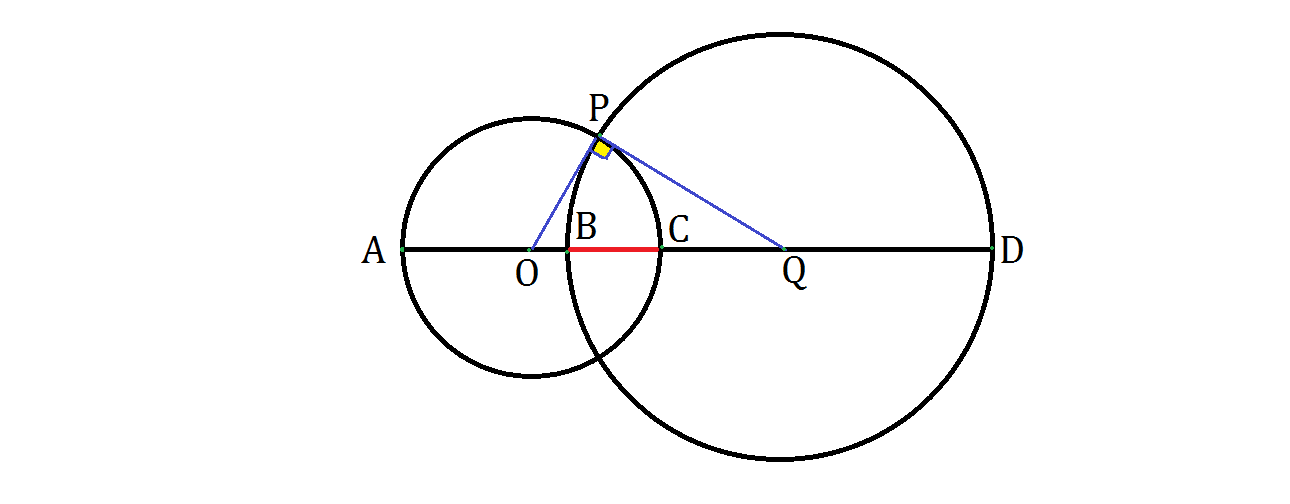
Two circles O and Q are orthogonal: their radii are perpendicular at their intersection point P , as shown above. Then the line A D is drawn such that it passes through both centers and intersects the arcs at points B and C .
If A B = 1 0 and C D = 2 4 , what is the length of the red segment B C ?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
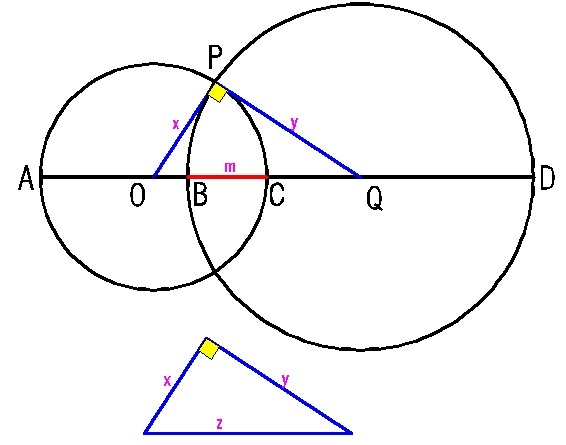 From the figure,
From the figure,
2 x = 1 0 + m ; x = 5 + 2 m
2 y = 2 4 + m ; y = 1 2 + 2 m
z = 1 0 + m + 2 4 − ( 5 + 2 m ) − ( 1 2 + 2 m ) = 1 7
By pythagorean theorem,
x 2 + y 2 = z 2
( 5 + 2 m ) 2 + ( 1 2 + 2 m ) 2 = 1 7 2
m 2 + 3 4 m − 2 4 0 = 0
Solving for m ,
m = B C = 6
Relevant wiki: Power of a Point
Let radius O P = r , P Q = R , and O Q = s . By Pythagorean theorem, s 2 = r 2 + R 2 .
The desired B C = R + r − s and A D = R + r + s .
Therefore, B D ⋅ A D = ( ( R + r ) − s ) ( ( R + r ) + s ) = ( R + r ) 2 − s 2 = 2 R r
Then A B = 1 0 = 2 r − ( R + r − s ) = r − R + s , and C D = 2 4 = 2 R − ( R + r − s ) = R − r + s .
Hence, A B ⋅ C D = ( s − ( R − r ) ) ( s + ( R − r ) ) = s 2 − ( R − r ) 2 = 2 R r .
That means A D ⋅ B C = A B ⋅ C D = 2 4 0 .
Suppose B C = x .
Then x ( x + 1 0 + 2 4 ) = 2 4 0 .
x 2 + 3 4 − 2 4 0 = 0
( x − 6 ) ( x + 4 0 ) = 0
Thus, x = 6 .
For the radii, r = 2 1 0 + 6 = 8 ; R = 2 2 4 + 6 = 1 5 .
Finally, s = 8 2 + 1 5 2 = 1 7 .
Note : The ratios along points A , B , C , D are called Harmonic range .
Relevant wiki: Power of a Point
( O P ) 2 = ( O B ) ( O D )
but O B = 1 0 − O P (since A O = O P ) and O D = O P + 2 4 (since O C = O P ), therefore
( O P ) 2 = ( 1 0 − O P ) ( O P + 2 4 )
( O P ) 2 = 1 0 ( O P ) + 2 4 0 − ( O P ) 2 − 2 4 ( O P )
2 ( O P ) 2 + 1 4 ( O P ) − 2 4 0 = 0
( O P ) 2 + 7 ( O P ) − 1 2 0 = 0
( O P + 1 5 ) ( O P − 8 ) = 0
O P = − 1 5 or O P = 8 (reject the negative value)
So O P = 8
It follows that B C = 2 ( 8 ) − 1 0 = 6
Alternate Solution: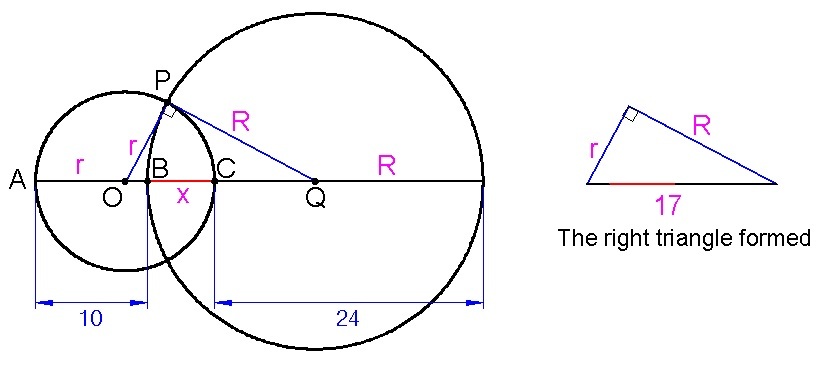 let
d
and
r
be the diameter and radius of the small circle respectively; let
D
and
R
be the diameter and radius of the big circle respectively; let
x
be the length of the red line
let
d
and
r
be the diameter and radius of the small circle respectively; let
D
and
R
be the diameter and radius of the big circle respectively; let
x
be the length of the red line
From the figure, d = 1 0 + x , therefore r = 5 + 2 x and D = 2 4 + x , therefore R = 1 2 + 2 x
O B = 1 0 − r = 1 0 − ( 5 + 2 x ) = 5 − 2 x
Q C = 2 4 − R = 2 4 − ( 1 2 + 2 x ) = 1 2 − 2 x
The length of the hypotenuse of the right triangle is therefore, O Q = 5 − 2 x + x + 1 2 − 2 x = 1 7
Applying pythagorean theorem in the right triangle, we have
1 7 2 = r 2 + R 2 ⟹ 2 8 9 = ( 5 + 2 x ) 2 + ( 1 2 + 2 x ) 2 ⟹ 2 8 9 = 2 5 + 5 x + 4 x 2 + 1 4 4 + 1 2 x + 4 x 2
After simplifying, the result is a quadratic equation
x 2 + 3 4 x − 2 4 0
solving for x using the quadratic formula gives
x = 6