Orthogonal parabolas
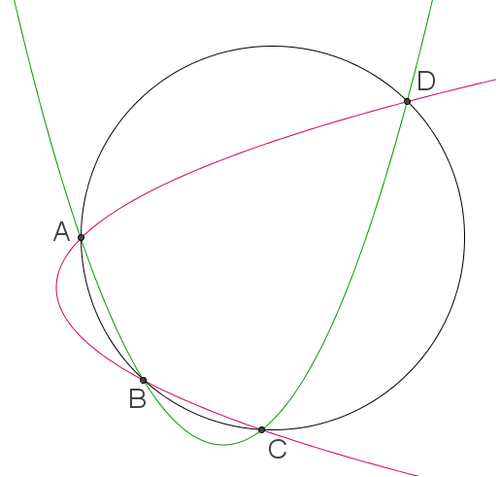 The two orthogonal parabolas
{
y
=
(
x
+
1
)
2
(
y
−
2
.
5
)
2
=
x
+
4
intersect at four distinct points,
A
=
(
x
1
,
y
1
)
,
B
=
(
x
2
,
y
2
)
,
C
=
(
x
3
,
y
3
)
and
D
=
(
x
4
,
y
4
)
. Let
S
=
x
1
+
x
2
+
x
3
+
x
4
and
R
=
y
1
+
y
2
+
y
3
+
y
4
. Find the value of
⌊
1
0
0
0
(
R
+
S
)
⌋
.
The two orthogonal parabolas
{
y
=
(
x
+
1
)
2
(
y
−
2
.
5
)
2
=
x
+
4
intersect at four distinct points,
A
=
(
x
1
,
y
1
)
,
B
=
(
x
2
,
y
2
)
,
C
=
(
x
3
,
y
3
)
and
D
=
(
x
4
,
y
4
)
. Let
S
=
x
1
+
x
2
+
x
3
+
x
4
and
R
=
y
1
+
y
2
+
y
3
+
y
4
. Find the value of
⌊
1
0
0
0
(
R
+
S
)
⌋
.
Remark : If the orthogonal parabolas intersect at four distinct points, then these four points are always on a same circle.
This problem is part of Curves... cut or touch? .
The answer is 6000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
The floor function had me thinking R+S was not an integer and that the problem was harder than it actually was.
It is given { y = ( x + 1 ) 2 ( y − 2 . 5 ) 2 = x + 4 .
Eliminating the y , we have ( ( x + 1 ) 2 − 2 . 5 ) 2 = x + 4 , which yields x 4 + 4 x 3 + … = 0 . This means that S = − 4 , by Vieta's Formula.
On the other hand, Eliminating the x gives y = ( ( y − 2 . 5 ) 2 − 4 + 1 ) 2 , which yields y 4 − 1 0 y 3 + … = 0 . This means that R = 1 0 , by Vieta's Formula.
Now ⌊ 1 0 0 0 ( R + S ) ⌋ = 6 0 0 0 .