Orthogonal tetrahedron
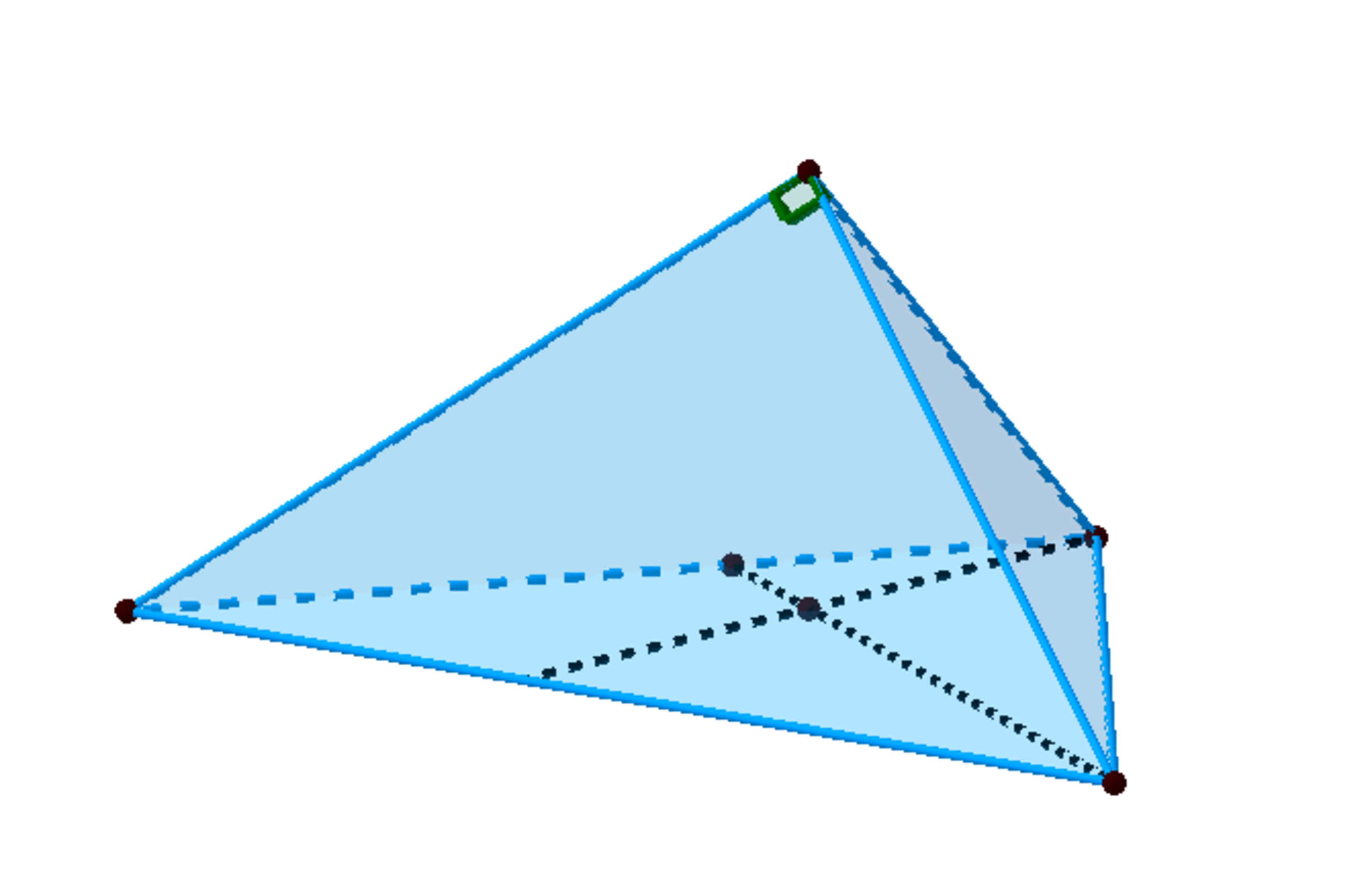
An orthogonal tetrahedron is created by cutting off one corner of a cube containing cube vertex . Tetrahedron's base is with orthocenter . Foot of the altitude from vertex is .
. The volume of the tetrahedron is . Find .
The answer is 207.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let E , F denote feet of the altitudes from B , C respectively.
Tetrahedron's net looks like this:
The height of the tetrahedron is the geometric mean of A H and H D . h = A H × H D = 6 .
A H × H D = B H × H E ⇒ H E = 6 .
A D H D B E H E C F H F = 1 ⇒ H F = 6 7 2 1 , C H = 2 2 1 , C F = 2 0 7 2 1
h a = 1 5 , h b = 1 2 , h c = 2 0 7 2 1
To calculate area of △ A B C we can use the formula using altitudes:
H r = ( h a − 1 + h b − 1 + h c − 1 ) / 2
A r e a − 1 = 4 H r ( H r − h a − 1 ) ( H r − h b − 1 ) ( H r − h c − 1 ) ⇒ △ A B C = 3 6 0
V = 3 6 × 3 6 0 = 1 2 0 3 ≈ 2 0 7 . 8 5