Oscillating block in liquid
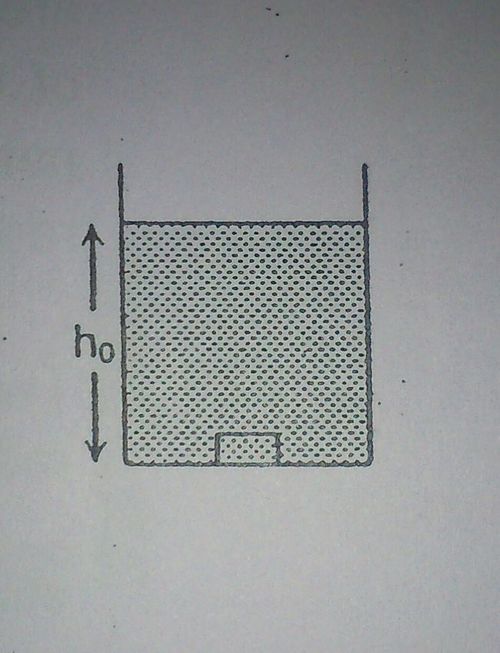 The container shown contains a liquid of variable density which varies as
, where
is total height of container,
is constant and
is measured from the bottom of the container. A solid block whose density is
and mass 'm' is released from bottom of the container. Given that block will execute SHM and is time period can be written as
The container shown contains a liquid of variable density which varies as
, where
is total height of container,
is constant and
is measured from the bottom of the container. A solid block whose density is
and mass 'm' is released from bottom of the container. Given that block will execute SHM and is time period can be written as
and is acceleration due to gravity. Find .
Details and Assumptions
- Assume block to be cubical.
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
m a = F b − m g m a = V d o ( 4 − h 3 y ) g − m g V = 5 d 0 2 m ⇝ a = 5 3 g − 5 h 6 g y = − 5 h 6 g ( y − 5 3 g ) a = 5 h 6 g ( Y ) T = 2 π 6 g 5 h