Oscillating wire
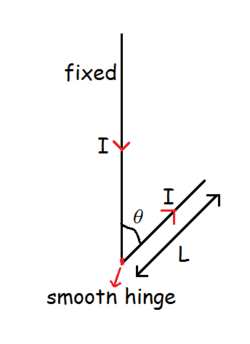 The arrangement shown is kept in an insulating liquid of density twice that of the identical wires making angle
with each other and carrying current
each, such that the tilted wire is free to rotate about the smooth hinge. The vertical wire is very long and is kept fixed. It is observed that the smaller wire of length
is in equilibrium at
.
The arrangement shown is kept in an insulating liquid of density twice that of the identical wires making angle
with each other and carrying current
each, such that the tilted wire is free to rotate about the smooth hinge. The vertical wire is very long and is kept fixed. It is observed that the smaller wire of length
is in equilibrium at
.
Now, the smaller wire is turned through a small angle in the vertical plane and released. Find the time period of its oscillations.
Details and assumptions :
-
-
The answer is 1.33806.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we find the torque due to the magnetic force , that will be equal to torque of (gravity and buoyant force) at equilibrium.
Clearly, as density of liquid is 2 ρ , the net force except magnetic force is 2 m g − m g = m g upwards, creating an anticlockwise torque of m g 2 L sin θ about hinge.
Consider a small element of length d x , at a distance x from the hinge on the smaller element. The magnetic force on this element is shown.
Clearly, the magnetic field here due to long wire is given by :
B = 2 π x sin θ μ 0 I ( 2 1 + cos θ ) out of the plane.
The force on the element is as shown,
d F = I B d x = 2 π x sin θ μ 0 I 2 ( 2 1 + cos θ ) d x
Hence, d τ B = x d F B = 4 π sin θ μ 0 I 2 ( 1 + cos θ ) d x
⇒ d τ B = 4 π μ 0 I 2 cot 2 θ d x
Thus, τ B = 4 π μ 0 I 2 L cot 2 θ
At θ = 6 0 ∘ , the torques balance,
4 π μ 0 I 2 L cot 2 6 0 ∘ = m g 2 L sin 6 0 ∘
⇒ π μ 0 I 2 = m g
Put this value in the expression of torque due to magnetic force to get :
τ B = 4 m g L cot 2 θ
Hence, τ n e t = 4 m g L cot 2 θ − 2 m g L cos θ clockwise
Now, when displaced by small angle ϕ , Wire would restore. Differentiate above expression to get
ϕ δ τ n e t ≈ − 8 m g L csc 2 2 θ − 2 m g L cos θ
Since, initially, τ n e t = 0 , δ τ n e t = τ n e t
At θ = 6 0 ∘ ,
δ τ n e t = τ n e t = 4 − 3 m g L ϕ
Hence, 3 m L 2 ϕ ¨ = − 4 3 m g L ϕ
Hence, we get T = 9 g 4 L
Substitute the values to get T ≈ 1 . 3 3 8 0 6 s