Oscillations of a triatomic molecule
Consider the following model of a triatomic molecule: Three point-charges with charge
q
and mass
m
are connected by massless rigid rods of length
l
. Clearly, the molecule is in equilibrium when the charges are aligned. Since this equilibrium is stable, the molecule can oscillate as shown in the figure. If the parameters
q
,
m
, and
l
satisfy
m
l
3
k
q
2
=
1
0
4
s
−
2
where
k
=
4
π
ϵ
0
1
,
find the period
T
in seconds
of small oscillations.
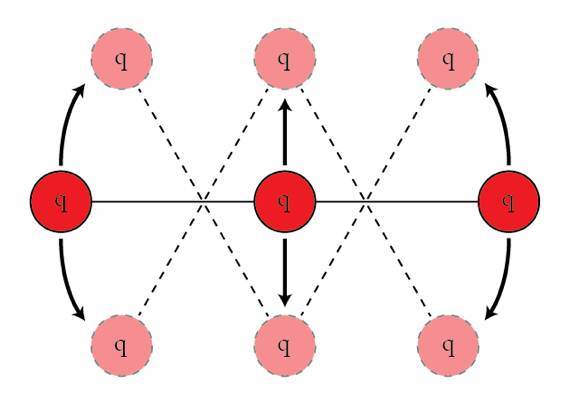
The answer is 0.0725.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Consider when the rods make an angle of (a) with the horizontal line (a is small). So the distance between two side charges is d= 2 l cos(a) = 2 l (1-(a^2)/2) (because a is small).
Set v1 is the speed of the center charge, v2=v3 are the speed of the side charges. Because the oscillations are small, we assume that the charges only move vertically. Because the center of mass do not move, m v1= m v2+m v3. So that v1=2v2=2v3. We have v12 = l a' (a' = da/dt) or v1+v2=l a'. So v1=2 l a'/3, v2=v3=l a'/3.
The energy of the system: E= m/2 (v1^2+v2^2+v3^2)+2 k q^2/l+k q^2/d or E=m/2 l^2 a'^2 (4/9+1/9+1/9) + 2 k q^2/l + k q^2/(1-a^2/2). Because a is small, E=m/3 l^2 a'^2 + 2 k q^2/l + k q^2 (1+a^2/2). Because E is constant, E'=0 or 2/3 m l^2 a' a'' + k q^2 a a'/(2 l) = 0. So a'' + 3 k q^2 a/(4 m l^3) = 0 So that the period T = 2 pi [(4 m l^3)/(3 k*q^2)]^(1/2) = 0.07255 (s)
number the charge 1 to 3 from left to right take the equilibrium position of the charges as origin O. From the conservation of momentum, we obtain that v {1}=v {3}=v {2}/2 or x'=x' {1}=x' {3}=x' {2}/2. Moreover, we obtain the deviation og each charge as x=x {1}=x {3}=x_{2}/2 During oscillation, interaction energy between 1&2, 2&3 are unchanged (since the distance is unchanged). However, the distance between 1 & 3 as E=\frac{kq^2}{sqrt{l^{2}-(3x)^2}}=kq^2 (1+9x^2/l^2)/l equation of energy conservation: m(x'^2+x'^2+(2x')^2) + kq^2 (1+9x^2/l^2)/l = const Take the derivative: 6mx'+\frac{9}{2}\frac{kq^2}{l^3}x=0 from that we can calculate the period is T= 0.07255s
Since the molecule is isolated (no external forces), the velocity of the center of mass of the molecule must be constant. Without loss of generality, we can assume that
v
C
M
=
0
and
R
C
M
=
0
. Let us denote the displacement of the charges 1 and 2 by
x
as shown in the figure below.
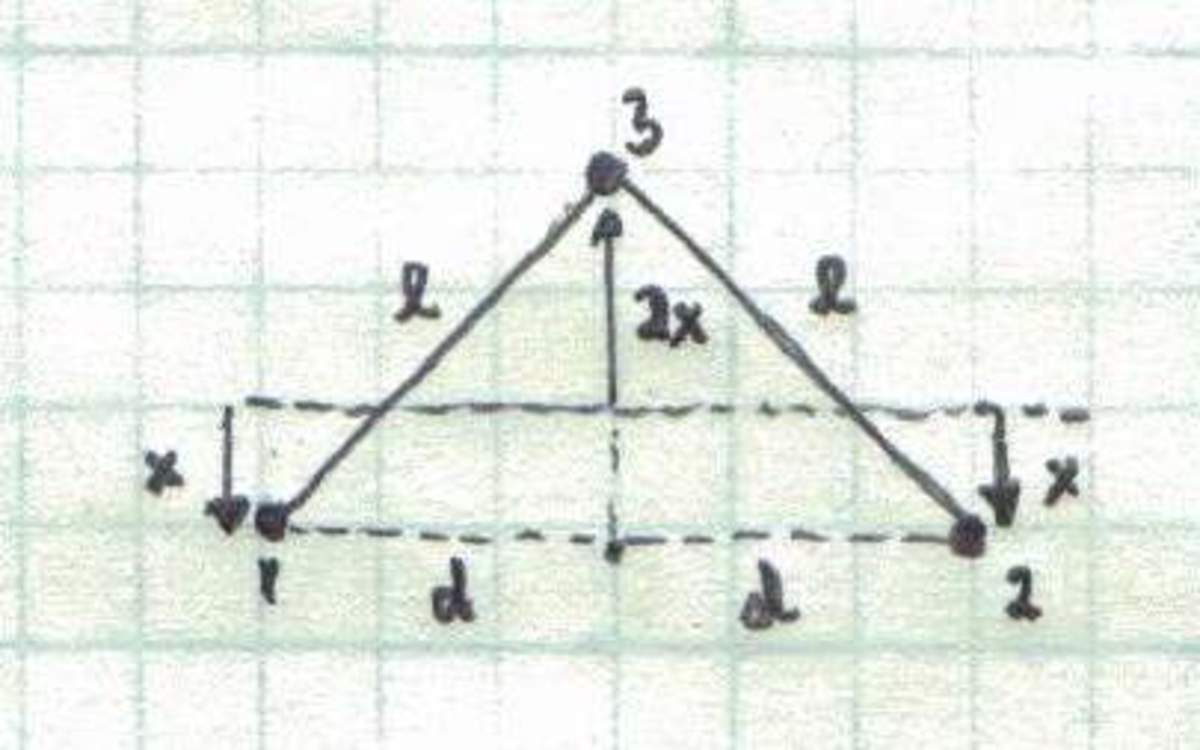
Then, the displacement of the charge 3 must be 2 x which ensures that position of the center of mass is zero. That is to say 3 m − 2 m x + m ( 2 x ) = 0 . Invoking the Pythagorean theorem and assuming that x ≪ l (small oscillations) we obtain d = l 2 − ( 3 x ) 2 = l 1 − ( 3 x / l ) 2 ≈ l ( 1 − 2 9 l 2 x 2 ) Now, we write the total kinetic energy of the system K = 2 2 m x ˙ 2 + 2 m ( 2 x ˙ ) 2 + 2 2 m ( d ˙ ) 2 ≈ 3 m x ˙ 2 and the total potential energy U = 2 d k q 2 + 2 l k q 2 ≈ 4 l 3 9 k q 2 x 2 + constant term . Note that we have only kept the quadratic terms x 2 and x ˙ 2 . We can neglect higher powers of x and x ˙ because the oscillations are small. The total energy of the oscillating molecule can be written as E = 2 M e q x ˙ 2 + 2 K e q x 2 + constant term where M e q = 6 m and K e q = 2 l 3 9 k q 2 . Examining the above expression we note that the molecule behaves just as a harmonic oscillator! Therefore, the period of oscillations is T = 2 π K e q M e q = 2 π 3 k q 2 4 m l 3 = 0 . 0 7 2 5 s .
Since the oscillation is small, we can assume the center of mass is always in the middle. Let the displacement of the middle charge from the equilibrium position be y , then the displacements of two charges at the two ends are − 2 1 y .
Let’s now analyse the force experienced by the middle charge. It experiences four forces, two are the repulsive forces from the charges at the two ends, two are the tensile forces due to the rods.
Assume the line joining the middle charge and the charge at the end makes an angle of θ with the horizontal. The electrostatic repulsion is l 2 k q 2 . Let the tensile force be F .
Since the rod is rigid, the acceleration at the two ends of a rod along the direction of the rod must be the same.
The acceleration of the middle charge along the direction of one rod is l 2 k q 2 − F − ( l 2 k q 2 − F ) cos 2 θ .
Since the oscillation is very small, cos 2 θ ≈ 1 . Hence the aaceleration of the middle charge along the direction of one rod ≈ 0 .
At one end of the rod, the charge experiences three forces, two repulsive forces from the other two charges and one tensile force from the rod. The acceleration at the end along the direction of the rod is
F − l 2 k q 2 − ( 2 l cos θ ) 2 k q 2 ≈ F − l 2 k q 2 − 4 l 2 k q 2
⟹ F = 4 l 2 5 k q 2
The acceleration of the middle charge in the y -direction is 2 ( m l 2 k q 2 − m F ) sin θ = 2 ( − 4 m l 2 k q 2 ) sin θ , where sin θ = l y + 2 1 y = 2 l 3 y
Hence, the acceleration is − 4 m l 3 3 k q 2 y
This shows the oscillation is a simple harmonic motion, and the period is thus 4 m l 3 3 k q 2 2 π = 0 . 0 7 2 5 5 s