Oscilloscope
An electron enters an oscilloscope exactly in the middle (between the plates, it will accelerate the electron vertically) with velocity . The plates are each long and away from the screen. At what angle will the electron leave the oscilloscope and how far (vertically) ( ) from its original course (dashed line) will it be when it hits the screen?
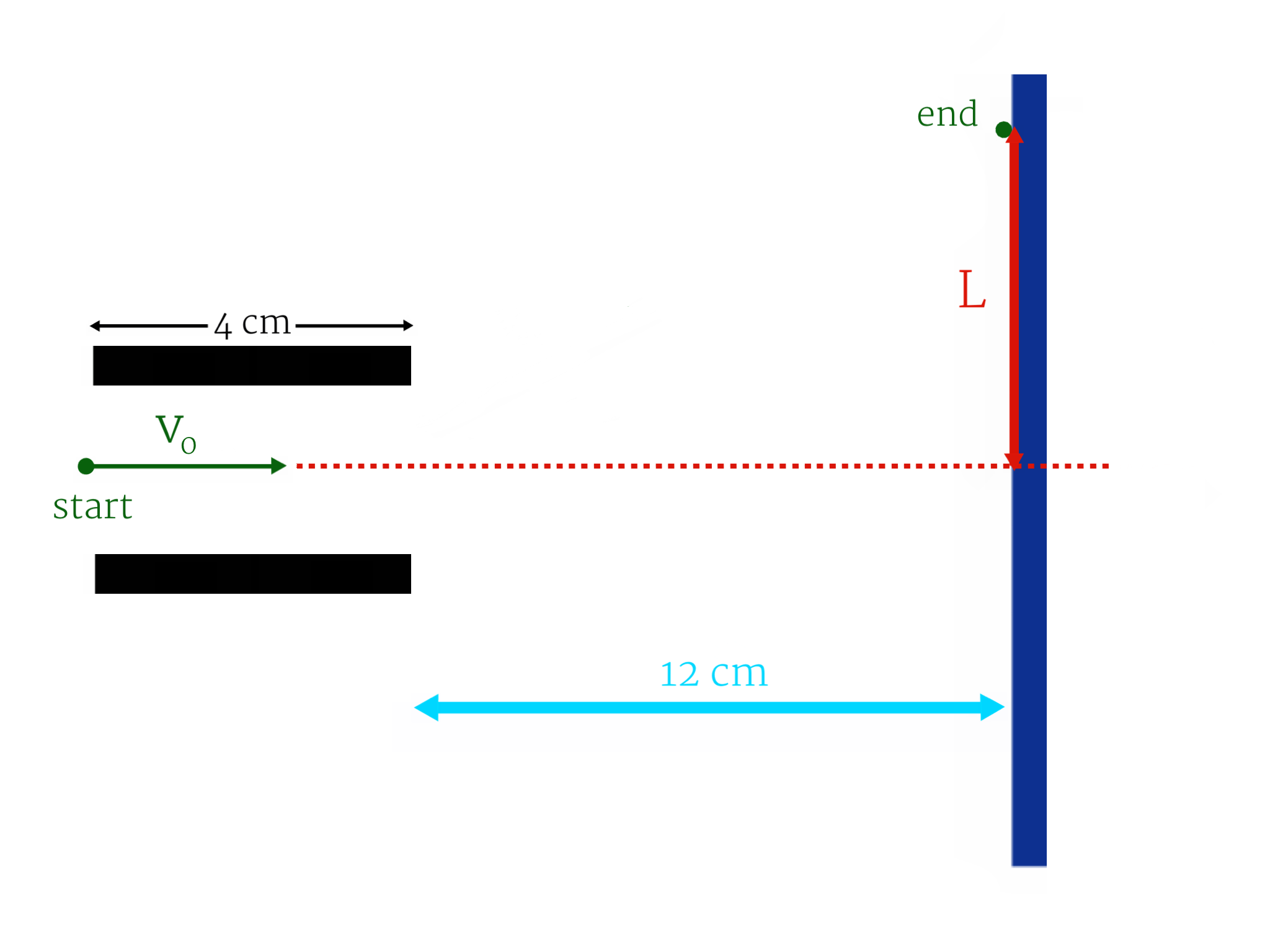
The strength of the electric field between the plates is .
( , )
Give your answer in the form (to nearest degree) + (to nearest cm).
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The magnitude of the force on the electron is F = E e = 6 0 0 0 N/C ⋅ 1 . 6 ⋅ 1 0 − 1 9 C = 9 . 6 ⋅ 1 0 − 1 6 N .
The acceleration is a = m F = 9 . 1 ⋅ 1 0 − 3 1 kg 9 . 6 ⋅ 1 0 − 1 6 N ≈ 1 . 0 5 ⋅ 1 0 1 5 m/s 2
Since the motion is accelerated we must use instantaneous velocities to find the angle. We can use 2 a s = v 0 2 + v f 2 to get the vertical component. We already have the horizontal component v 0 which equals 8 ⋅ 1 0 6 m/s . The initial vertical component is 0.
The distance travelled is s = 2 a t 2 and we can get the time by looking at the horizontal components: t = v 0 x = 8 ⋅ 1 0 6 m/s 0 . 0 4 m = 5 ⋅ 1 0 − 9 s
Solving, we get s = 1 . 3 1 2 5 cm and the acceleration is a = 1 . 0 5 ⋅ 1 0 1 5 m/s 2 .
v f = 2 a s = 2 ⋅ 1 . 0 5 ⋅ 1 0 1 5 m/s 2 ⋅ 0 . 0 1 3 1 2 5 m = 5 . 2 5 ⋅ 1 0 6 m/s .
The angle is therefore tan α = v 0 v f → α = arctan ( 0 . 6 5 6 2 5 ) → α = 3 3 . 2 7 ° ≈ 3 3 °
The electron will not be affected by the acceleration anymore since it left the oscilloscope so it will keep the instantaneous velocities we just calculated. Time needed to reach the screen from this point is t s = v 0 D = 1 . 5 ⋅ 1 0 − 8 s .
The additional vertical distance from the original course is s s = v f t s = 7 . 8 7 5 cm
Total: L = s + s s = 1 . 3 1 2 5 cm + 7 . 8 7 5 cm = 9 . 1 8 7 5 cm ≈ 9 cm
So the answer is α + L = 3 3 + 9 = 4 2