Out of the oven, into the frying pan

Classical Mechanics Level 4

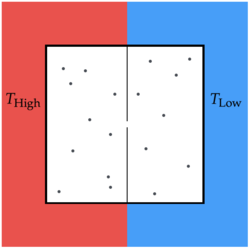Consider a gas in the device shown above. Two halves of the box are separated by a dividing wall that has a small hole in it, which is just slightly wider than the diameter of the gas molecules. Each half of the box is in contact with a heat bath held at a given temperature.

If there are $N$ gas molecules in the box, find the expected number of gas molecules in the hot side when the box reaches steady state.

Assumptions and Details

$N=100,000$
$T_\text{High}=700\text{ K}$
$T_\text{Low}=200\text{ K}$

The answer is 34833.147735479.

1 solution

Katarina Petrović
Aug 1, 2015

First we assume that the amounts of molecules in each part are respectively $nm_1$ and $nm_2$ , than we have: $nm_1+nm_2=N/N_a$ where $N_a$ is Avogadro's constant.

In the steady state we have following relations: $\begin{aligned} \Delta N_1&=\Delta N_2 \\ nm_1Sv_1t&=nm_2Sv_2t \end{aligned}$

where $S$ is an area of the hole, $v_1$ and $v_2$ the average speeds of the molecules in each part, $t$ a small time interval, and $\Delta N_1$ and $\Delta N_2$ are the numbers of molecules which pass through the hole during the interval $t$ .

After calculating this we get a relation: $nm_1\sqrt{T_1}=nm_2\sqrt{T_2}$ and therefore: $N_1=N\frac{\sqrt{T_2}}{\sqrt{T_1}+\sqrt{T_2}}=34833.148\text{ K}$ (using $N_1=nm_1N_a)$

The question could precise the definition of "steady state". I interpreted steady state as no more movements between half boxes (equilibrium reached). At that state, with x number of molecules in hot half box & y number of molecules in cold half box: x + y = N,
ideal gas: 700x = 200y (volume of each half boxes same so cancel out)
700x = 200(100,000 - x)
x = 22,222.22 gas molecules in hot half box
(assuming perfect insulation dividing wall and hot/cold bath)

michael de seguin - 4 years, 8 months ago

I agree with Michael De Seguin. The steady state means pressure in both chambers are equal. The problem then reduces to applying gas equation of state and hot chamber has (200/900) 100000=22222.2 molecules and cold chamber has (700/900) 100000=77777.8 molecules.

Vinod Kumar - 3 years ago

I also agree with the last two comments. Moreover, there are some small mistakes in the solution: N is the number of molecules. It is a pure number, so its unit cannot be kelvin. n = N / N_a (whose unit is the mole) is called amount of substance, chemical amount etc. but not "amount of molecules".

Giacomo Lanza - 2 years, 3 months ago

Even I got x = 22222.222 gas molecules.

Puneet Pinku - 1 year, 3 months ago

Out of the oven, into the frying pan

The answer is 34833.147735479.

1 solution

0 pending reports