Over The Top!
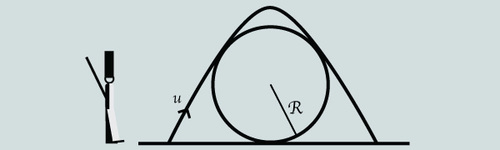 Gabriel the Grenadier wants to lob a grenade over a huge barrier in front of him. He models the scenario in the following way:
Gabriel the Grenadier wants to lob a grenade over a huge barrier in front of him. He models the scenario in the following way:
The grenade is a point mass that is thrown with a variable velocity , at a variable angle . The barrier is a cylinder with a radius of .
Find the minimum value of (in m/s) for which the particle crosses the log.
Details and assumptions
Neglect air resistance and viscosity.
Take
.
The answer is 9.728.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
When, we throw the particle with minimum required velocity, it touches the cylinder at two points. Let us say the line joining center of cylinder and particle makes an angle ϕ with horizontal, and at this time speed is v . Clearly, height scaled is h = R ( 1 + sin ϕ ) .
Using conservation of energy,
v 2 = u 2 − 2 g h = u 2 − 2 g R ( 1 + sin ϕ )
Now, the range of particle if it is thrown from this point with speed v is :
x = g v 2 sin 2 ( 2 π − ϕ ) = g ( u 2 − 2 g R ( 1 + sin ϕ ) ) sin 2 ϕ
Now, this should be same as 2 R cos ϕ . as the distance between two points where particle touches cylinder is 2 R cos ϕ
Hence, g ( u 2 − 2 g R ( 1 + sin ϕ ) ) sin 2 ϕ = 2 R cos ϕ
⇒ u 2 = g R ( 2 + 2 sin ϕ + sin ϕ 1 ) ≥ 2 g R ( 1 + 2 ) ( AM-GM)
Thus , u ≥ 9 . 7 2 8 m / s