Overlap Area

Calculus Level 4

Shape $1$ is an ellipse:

$\large{\frac{x^2}{4} + \frac{y^2}{1} = 1}$

Shape $2$ is a square of side length $3$ with its center at $(x,y) = (3,-1)$ . The square's sides are aligned with the vectors $(u_x,u_y) = \Big(\cos (-\pi/3), \sin (-\pi/3) \Big)$ and $(v_x,v_y) = \Big(\cos (\pi/6), \sin (\pi/6) \Big)$ .

If the overlapping area between the two shapes is $A$ , give your answer as $\lfloor 1000 A \rfloor$

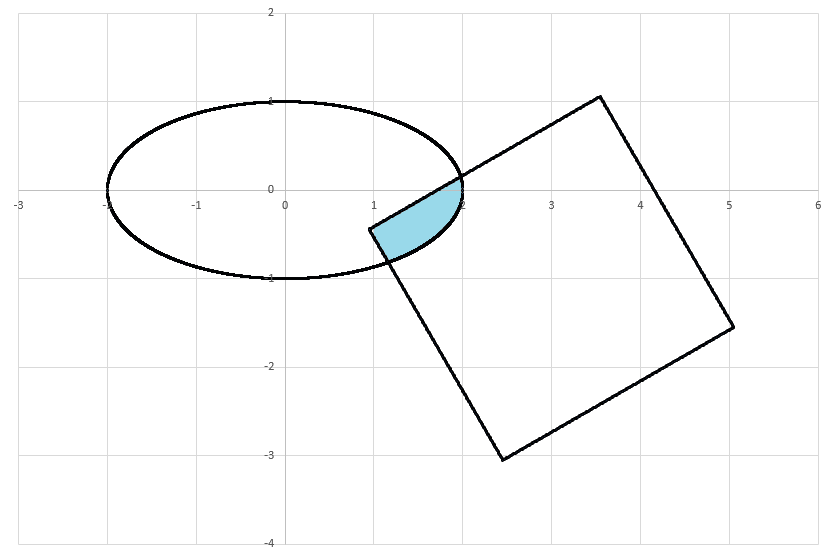
The answer is 455.

1 solution

Chris Lewis
Jun 3, 2019

Just an outline (I'm on my phone and the details are a bit messy!) I'll give a couple of decimal places along the way to act as a guide.

One solution is as follows:

find the coordinates of the vertex of the square that lies inside the ellipse $(0.95,-0.45)$
find the coordinates of the intersections of the square and ellipse $(1.98,0.14)$ and $(1.16,-0.81)$
scale the whole setup by a factor of $2$ vertically. This maps the ellipse to a circle, and the blue region to a triangle whose coordinates we know, and a circular segment whose radius and chord-length we know. It will also have the effect of doubling areas.
calculate the areas of the triangle ( $0.50$ ) and segment ( $0.41$ ) and sum these
divide by $2$ to get the area of the original blue region, $0.4552\ldots$

This gives the answer $\boxed{455}$ .

Overlap Area

The answer is 455.

1 solution

0 pending reports