Overlap of Congruent Triangles
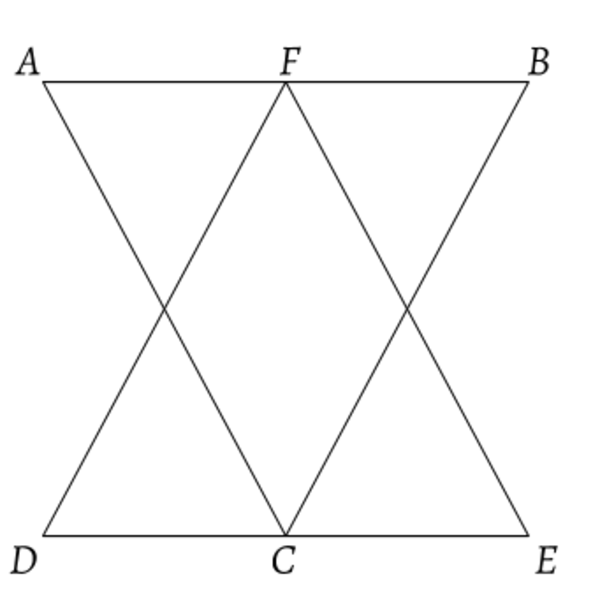
Two congruent isosceles triangles, A B C and D E F , overlap so that their bases are parallel and the vertex of each is the midpoint of the base of the other, as shown above.
If the area of the overlap is 12 cm 2 , how many cm 2 is △ A B C ?
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let ∣ A B ∣ = a and ∣ F C ∣ = h . Then the area of the overlapped region is 2 × 2 1 × 2 a × 2 h = 1 2 , or 2 1 a h = 2 4 . Therefore area of △ A B C is 2 4 c m 2
Due to symmetry, the overlapped figure is made of 6 congruent triangles as shown above. The overlap with an area of 12 cm 2 is made up of two of such triangles, therefore each triangle is 6 cm 2 . △ A B C is made of four such triangle and hence has an area of 6 × 4 = 24 cm 2 .