Overlapped Squares Troubles
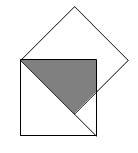 The figure above shows two overlapped squares of side
1
. Find the shaded area.
The figure above shows two overlapped squares of side
1
. Find the shaded area.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
very nice answer
how come EF=ED? although i too used it without proving :P
Log in to reply
F E D is a right angle, and E D F is a 4 5 degrees angle. It's an isosceles right triangle, and thus the reason why the sides have equal measure.
How come ED is square root 2 -1???????
Log in to reply
Diagonal =(1^2+1^2)^1/2=2^1/2, ED=Diagonal of the ABCD-Side of the other square, ED=2^1/2-1
ED = BD-BE
how do you know BE is 1?
Log in to reply
BE is one of the sides of a square. The side of the square is given as 1. So, BE is 1.
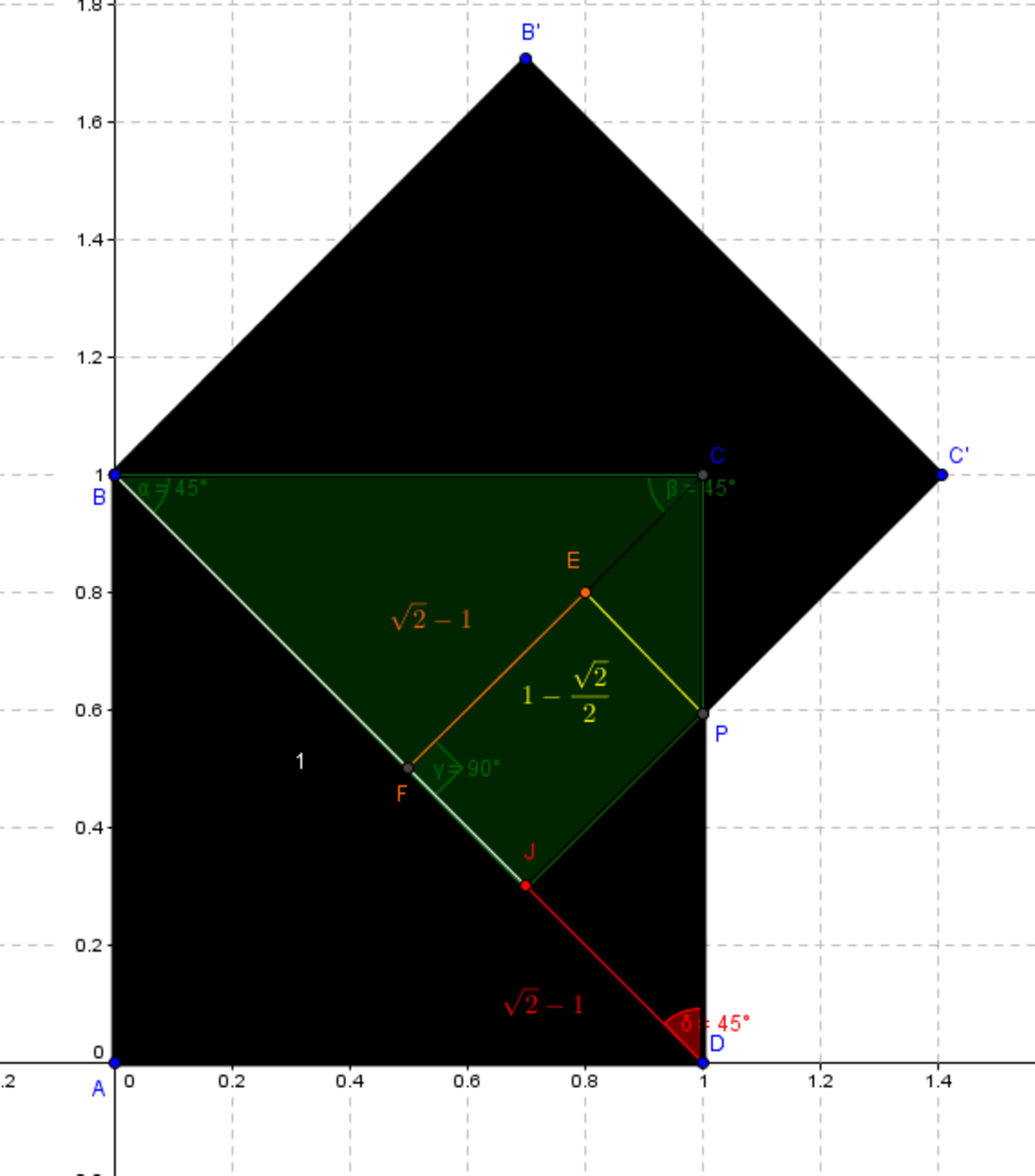
1. Plot segments BD and AC 2. BD and AC intersect at point F 3. BD= 2 4. BF= 2 2 5. FD = 2 2 6. CF = 2 2 7. BJ = 1 8. JD = 2 − 1 9. FJ = 2 2 − ( 2 − 1 ) = 1 − 2 2 10. Plot EP perpendicular to AC 11. E P ≅ F J 12. E P = 1 − 2 2 13 . J P ⊥ B D 14. J P ≅ J D 15. J P = 2 − 1 16. E C ≅ E P
17) Area of Shaded Region = Area of △ F B C + Area of △ E C P + Area of ▱ EFJP 18) Area of Shaded Region = 4 1 + ( 4 3 − 2 2 ) + ( 2 3 2 − 2 ) = 2 − 1
@Bruce Preston I liked your solution in the comment, so I converted it over into a solution.
Log in to reply
Thank you. I was trying to do that myself. I accidentally deleted a previous solution, but it wouldn't allow me to post a solution anymore. Thanks for converting it appreciate it.
nice! please let me know about the applications available to generate these graphs. :)
There's an intuitive guess with this problem due to the poor multiple choice options. I am quite lazy, so that's how I solved it quickly.
We know that the area of the shaded area must be less than 2 1 .
2 2 > 2 1 , thus not the answer.
3 − 2 , 3 seems impossible to get from the squares, therefore not a plausible answer.
2 2 + 1 > 2 1 , thus not the answer.
2 + 1 > 2 1 , thus not the answer.
2 − 1 < 2 1 , the only one that is plausible, thus the answer.
This is similar to the "quick way" I solved it.
(1/2) -(1/2) (square root of 2 - 1)^2 =
(square root of 2) - 1
B D 2 = 1 2 + 1 2 ⇒ B D = 2
E D = B D − 1 = 2 − 1
E F = 2 − 1
Shaded area is ∣ △ B C D ∣ − ∣ △ E D F ∣ .
∣ △ B C D ∣ = 2 1 × 1 = 2 1
∣ △ E D F ∣ = 2 E F × E D = 2 ( 2 − 1 ) 2 = 2 3 − 2 2
∣ △ B C D ∣ − ∣ △ E D F ∣ = 2 1 − 2 3 − 2 2 = 2 − 1 .