Overlapping Area
What is the maximal overlapping area between a circle and an equilateral triangle both with the same 1 cm 2 area ?
Submit the answer in cm 2 to 3 decimal places.
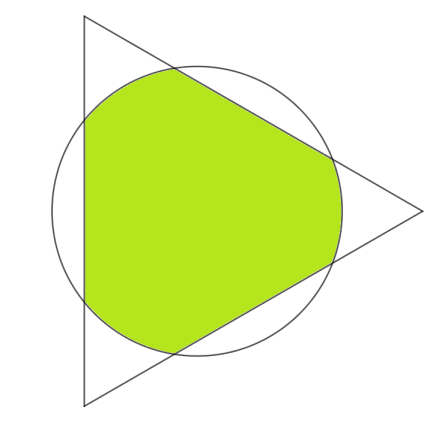
The answer is 0.818.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
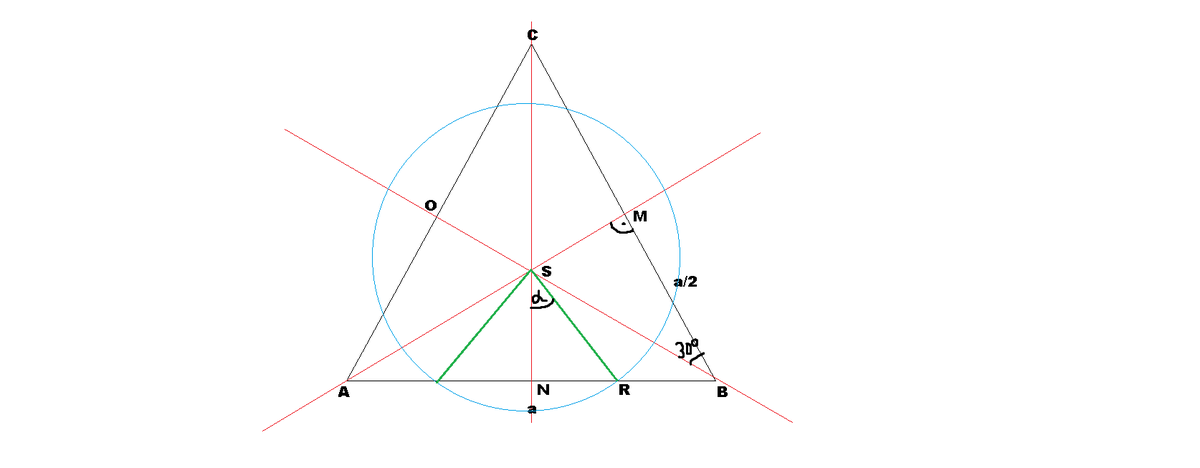 S
T
=
4
3
×
a
2
⇒
a
=
3
4
×
S
T
=
3
4
=
2
×
3
1
S
C
=
S
=
π
×
r
2
⇒
r
=
π
S
=
π
1
tan
(
3
0
)
=
2
a
∣
S
M
∣
=
a
2
×
∣
S
M
∣
⇒
∣
S
M
∣
=
2
a
×
tan
(
3
0
)
=
2
a
×
3
1
=
2
×
3
a
∣
C
M
∣
=
a
2
−
(
2
a
)
2
=
a
2
−
4
a
2
=
4
3
×
a
2
=
a
×
2
3
∣
C
S
∣
=
∣
C
M
∣
−
∣
S
M
∣
=
2
a
×
3
−
2
×
3
a
=
2
×
3
3
×
a
−
a
=
2
×
3
2
×
a
=
3
a
∣
N
S
∣
=
∣
C
S
∣
2
−
(
2
a
)
2
=
3
a
2
−
4
a
2
=
1
2
a
2
=
a
×
1
2
1
∣
N
R
∣
=
r
2
−
∣
N
S
∣
2
=
(
π
1
)
2
−
(
a
×
1
2
1
)
2
=
π
1
−
1
2
a
2
=
1
2
×
π
1
2
−
a
2
×
π
sin
(
α
)
=
r
∣
N
R
∣
⇒
α
=
arcsin
(
π
1
1
2
×
π
1
2
−
a
2
×
π
)
=
arcsin
(
1
2
×
π
1
2
×
π
−
a
2
×
π
2
)
=
arcsin
(
1
2
×
π
π
×
(
1
2
−
a
2
×
π
)
)
=
arcsin
(
1
2
1
2
−
a
2
×
π
)
=
arcsin
(
1
2
1
2
−
4
×
3
1
×
π
)
=
arcsin
(
1
2
×
3
1
2
×
3
−
4
×
π
)
=
arcsin
(
3
×
3
3
×
3
−
π
)
=
arcsin
(
2
7
2
7
−
π
)
=
arcsin
(
1
−
2
7
π
)
S
A
R
C
=
2
1
×
(
π
1
)
2
×
(
1
8
0
π
×
2
×
α
−
sin
(
2
×
α
)
)
=
2
×
π
1
×
(
1
8
0
π
×
2
×
α
−
sin
(
2
×
α
)
)
=
1
8
0
×
π
π
×
α
−
2
×
π
sin
(
2
×
α
)
=
1
8
0
×
π
π
×
α
−
9
0
×
sin
(
2
×
α
)
S
=
S
C
−
3
×
S
A
R
C
=
1
−
3
×
1
8
0
×
π
π
×
arcsin
(
1
−
2
7
π
)
−
9
0
×
sin
(
2
×
arcsin
(
1
−
2
7
π
)
)
∼
0
.
8
1
7
5
2
8
6
9
4
.
.
.
S
T
=
4
3
×
a
2
⇒
a
=
3
4
×
S
T
=
3
4
=
2
×
3
1
S
C
=
S
=
π
×
r
2
⇒
r
=
π
S
=
π
1
tan
(
3
0
)
=
2
a
∣
S
M
∣
=
a
2
×
∣
S
M
∣
⇒
∣
S
M
∣
=
2
a
×
tan
(
3
0
)
=
2
a
×
3
1
=
2
×
3
a
∣
C
M
∣
=
a
2
−
(
2
a
)
2
=
a
2
−
4
a
2
=
4
3
×
a
2
=
a
×
2
3
∣
C
S
∣
=
∣
C
M
∣
−
∣
S
M
∣
=
2
a
×
3
−
2
×
3
a
=
2
×
3
3
×
a
−
a
=
2
×
3
2
×
a
=
3
a
∣
N
S
∣
=
∣
C
S
∣
2
−
(
2
a
)
2
=
3
a
2
−
4
a
2
=
1
2
a
2
=
a
×
1
2
1
∣
N
R
∣
=
r
2
−
∣
N
S
∣
2
=
(
π
1
)
2
−
(
a
×
1
2
1
)
2
=
π
1
−
1
2
a
2
=
1
2
×
π
1
2
−
a
2
×
π
sin
(
α
)
=
r
∣
N
R
∣
⇒
α
=
arcsin
(
π
1
1
2
×
π
1
2
−
a
2
×
π
)
=
arcsin
(
1
2
×
π
1
2
×
π
−
a
2
×
π
2
)
=
arcsin
(
1
2
×
π
π
×
(
1
2
−
a
2
×
π
)
)
=
arcsin
(
1
2
1
2
−
a
2
×
π
)
=
arcsin
(
1
2
1
2
−
4
×
3
1
×
π
)
=
arcsin
(
1
2
×
3
1
2
×
3
−
4
×
π
)
=
arcsin
(
3
×
3
3
×
3
−
π
)
=
arcsin
(
2
7
2
7
−
π
)
=
arcsin
(
1
−
2
7
π
)
S
A
R
C
=
2
1
×
(
π
1
)
2
×
(
1
8
0
π
×
2
×
α
−
sin
(
2
×
α
)
)
=
2
×
π
1
×
(
1
8
0
π
×
2
×
α
−
sin
(
2
×
α
)
)
=
1
8
0
×
π
π
×
α
−
2
×
π
sin
(
2
×
α
)
=
1
8
0
×
π
π
×
α
−
9
0
×
sin
(
2
×
α
)
S
=
S
C
−
3
×
S
A
R
C
=
1
−
3
×
1
8
0
×
π
π
×
arcsin
(
1
−
2
7
π
)
−
9
0
×
sin
(
2
×
arcsin
(
1
−
2
7
π
)
)
∼
0
.
8
1
7
5
2
8
6
9
4
.
.
.
You have done a good job obtaining the answer. However many steps could be shortened.
α
=
arcsin
⎝
⎛
π
1
1
2
×
π
1
2
−
a
2
×
π
⎠
⎞
=
arcsin
⎝
⎛
1
2
1
2
−
3
4
×
π
⎠
⎞
=
arcsin
(
1
−
3
3
π
)
I missed since I took
α
i
n
p
l
a
c
e
o
f
2
α
.
. My solution is as under.

LaTeX:
S
T
=
4
3
×
a
2
⇒
a
=
3
4
×
S
T
=
3
4
=
2
×
3
1
S
C
=
S
=
π
×
r
2
⇒
r
=
π
S
=
π
1
tan
(
3
0
)
=
2
a
∣
S
M
∣
=
a
2
×
∣
S
M
∣
⇒
∣
S
M
∣
=
2
a
×
tan
(
3
0
)
=
2
a
×
3
1
=
2
×
3
a
∣
C
M
∣
=
a
2
−
(
2
a
)
2
=
a
2
−
4
a
2
=
4
3
×
a
2
=
a
×
2
3
∣
C
S
∣
=
∣
C
M
∣
−
∣
S
M
∣
=
2
a
×
3
−
2
×
3
a
=
2
×
3
3
×
a
−
a
=
2
×
3
2
×
a
=
3
a
∣
N
S
∣
=
∣
C
S
∣
2
−
(
2
a
)
2
=
3
a
2
−
4
a
2
=
1
2
a
2
=
a
×
1
2
1
∣
N
R
∣
=
r
2
−
∣
N
S
∣
2
=
(
π
1
)
2
−
(
a
×
1
2
1
)
2
=
π
1
−
1
2
a
2
=
1
2
×
π
1
2
−
a
2
×
π
α
=
arcsin
⎝
⎛
π
1
1
2
×
π
1
2
−
a
2
×
π
⎠
⎞
=
arcsin
⎝
⎛
1
2
1
2
−
3
4
×
π
⎠
⎞
=
arcsin
(
1
−
2
7
π
)
S
A
R
C
=
2
1
×
(
π
1
)
2
×
(
1
8
0
π
×
2
×
α
−
sin
(
2
×
α
)
)
=
2
×
π
1
×
(
1
8
0
π
×
2
×
α
−
sin
(
2
×
α
)
)
=
1
8
0
×
π
π
×
α
−
2
×
π
sin
(
2
×
α
)
=
1
8
0
×
π
π
×
α
−
9
0
×
sin
(
2
×
α
)
S
=
S
C
−
3
×
S
A
R
C
=
1
−
3
×
1
8
0
×
π
π
×
arcsin
(
1
−
2
7
π
)
−
9
0
×
sin
(
2
×
arcsin
(
1
−
2
7
π
)
)
∼
0
.
8
1
7
5
2
8
6
9
4
.
.
.
Above is the same program whose latex your editor has given. But your editor has inserted many many
unnecessary { } and \left \right, making it very difficult to follow. You may go for a better editor. Since I write
directly in latex I have no idea of any editor. One thing you can do even with your editor. After every \\ add three or more spaces and a return. In this way your lines even in latex will be separated. With best wishes.
Unsubscribe