Overlapping Points
points are placed evenly around a circle as shown in the picture below -
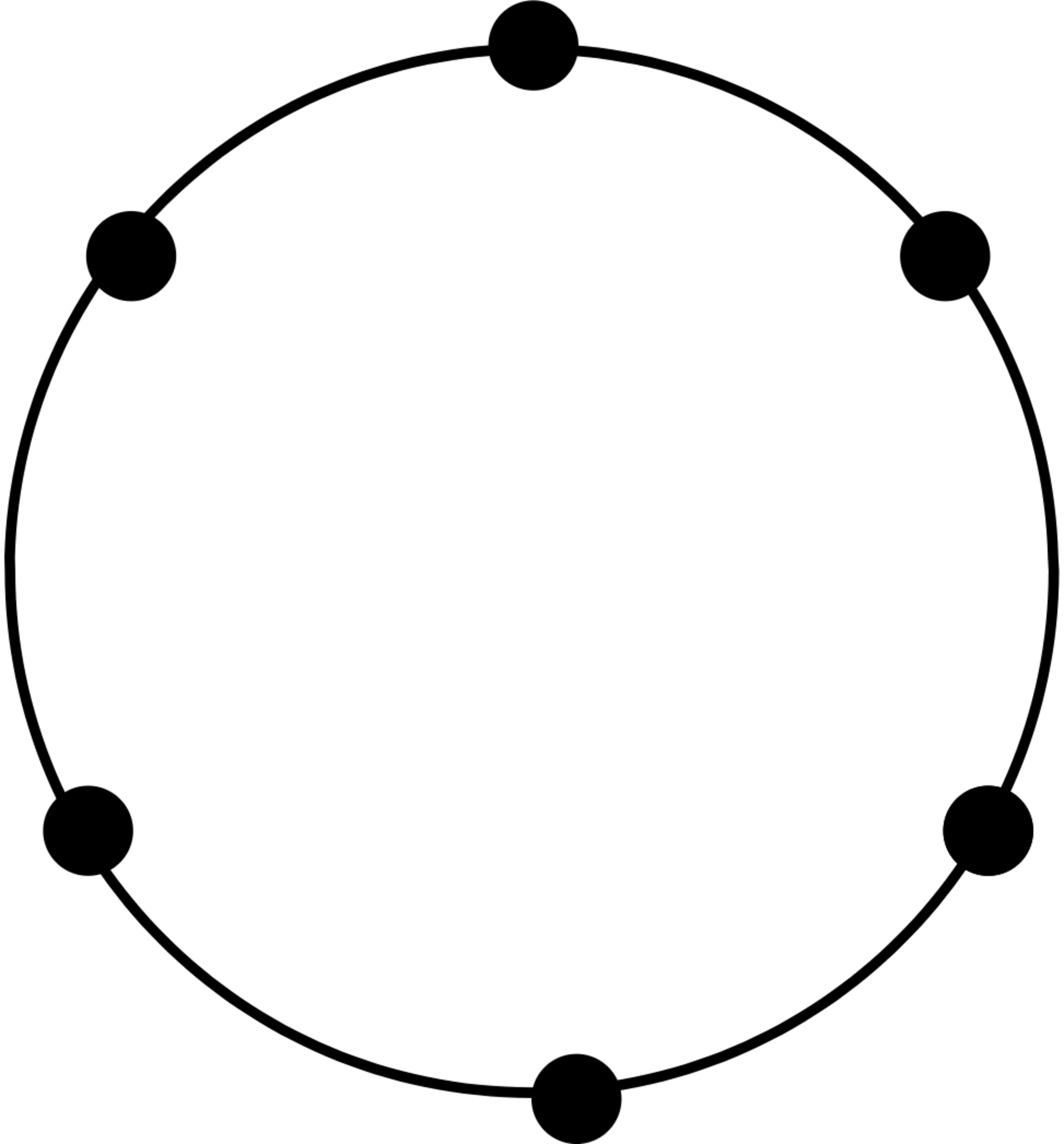 They are labeled
and
at random. What is the probability that the two triangles
and
do not overlap? Express your answer as a common fraction in simplest form.
They are labeled
and
at random. What is the probability that the two triangles
and
do not overlap? Express your answer as a common fraction in simplest form.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's redefine the problem in our own words. We can see that the problem is literally asking us, "What determines whether two angles overlap or not." Well, the triangles will not overlap if and only if A B C and D E F are all consecutive on the circle, as shown below -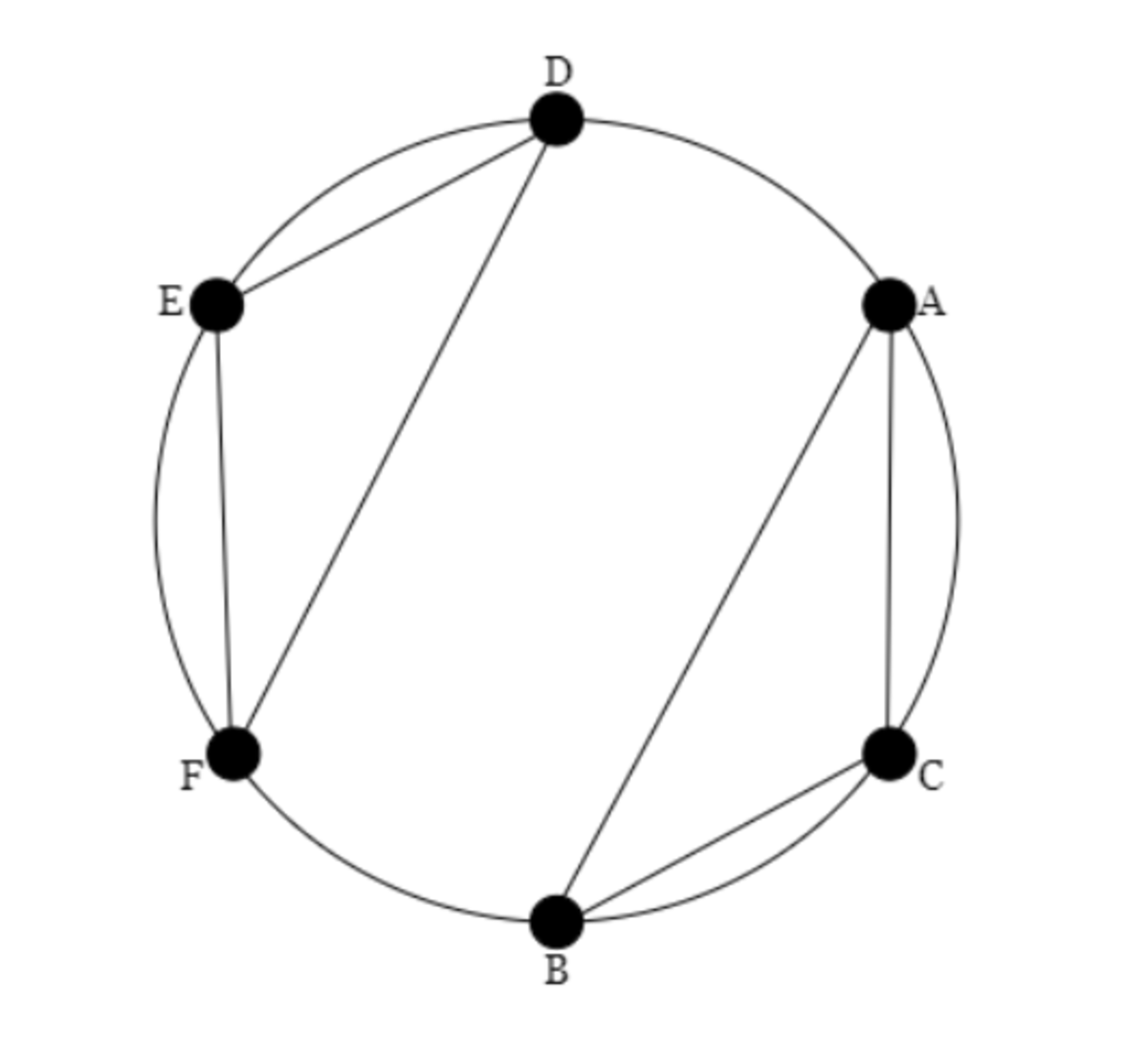 We can see if that the triangles are not consecutive on the circle, they will overlap. We can see that by using this diagram -
We can see if that the triangles are not consecutive on the circle, they will overlap. We can see that by using this diagram -
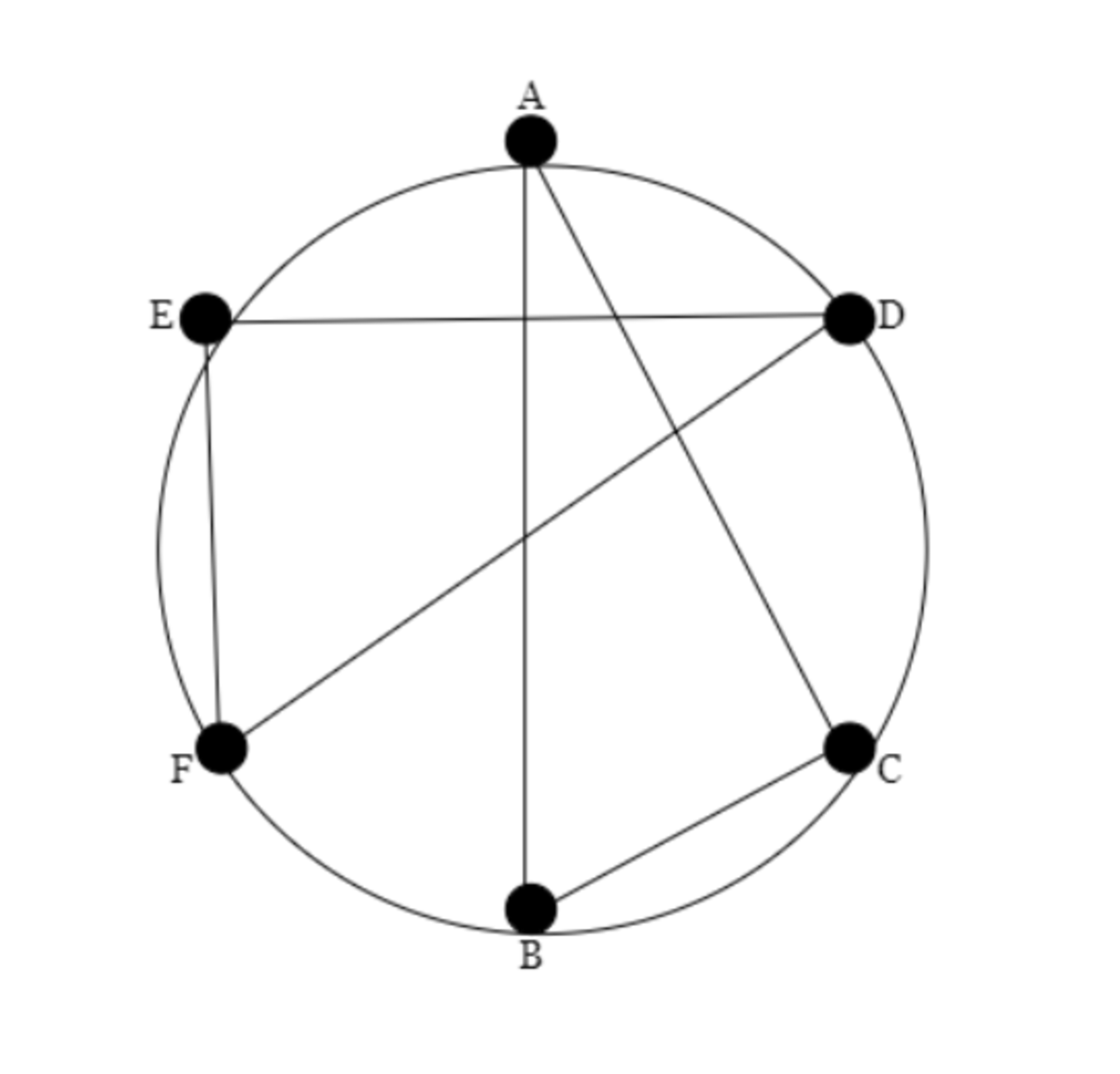 Now that we understand the circumstances, we can look for a suitable counting approach. We know how to count the number of ways to place labels on the
6
points. There are
6
ways to label the first points, then
5
ways remaining to label the second point, and so on. Thus, there are
6
!
ways to label the
6
points. However, we have over-counted, and therefore we will have to divide by
6
. Doing this will account for all the rotations. So there are really
6
6
!
=
5
!
=
1
2
0
total ways to arrange the labels.
Now that we understand the circumstances, we can look for a suitable counting approach. We know how to count the number of ways to place labels on the
6
points. There are
6
ways to label the first points, then
5
ways remaining to label the second point, and so on. Thus, there are
6
!
ways to label the
6
points. However, we have over-counted, and therefore we will have to divide by
6
. Doing this will account for all the rotations. So there are really
6
6
!
=
5
!
=
1
2
0
total ways to arrange the labels.
Next, we must count how many of the total arrangements have A B C all together and D E F all together. There are 3 ! = 6 ways to arrange D E F . This means that there are 6 × 6 = 3 6 ways to arrange A B C and D E F all together. Hence, the probability is 1 2 0 3 6 ⟹ 1 0 3