Overlapping Squares
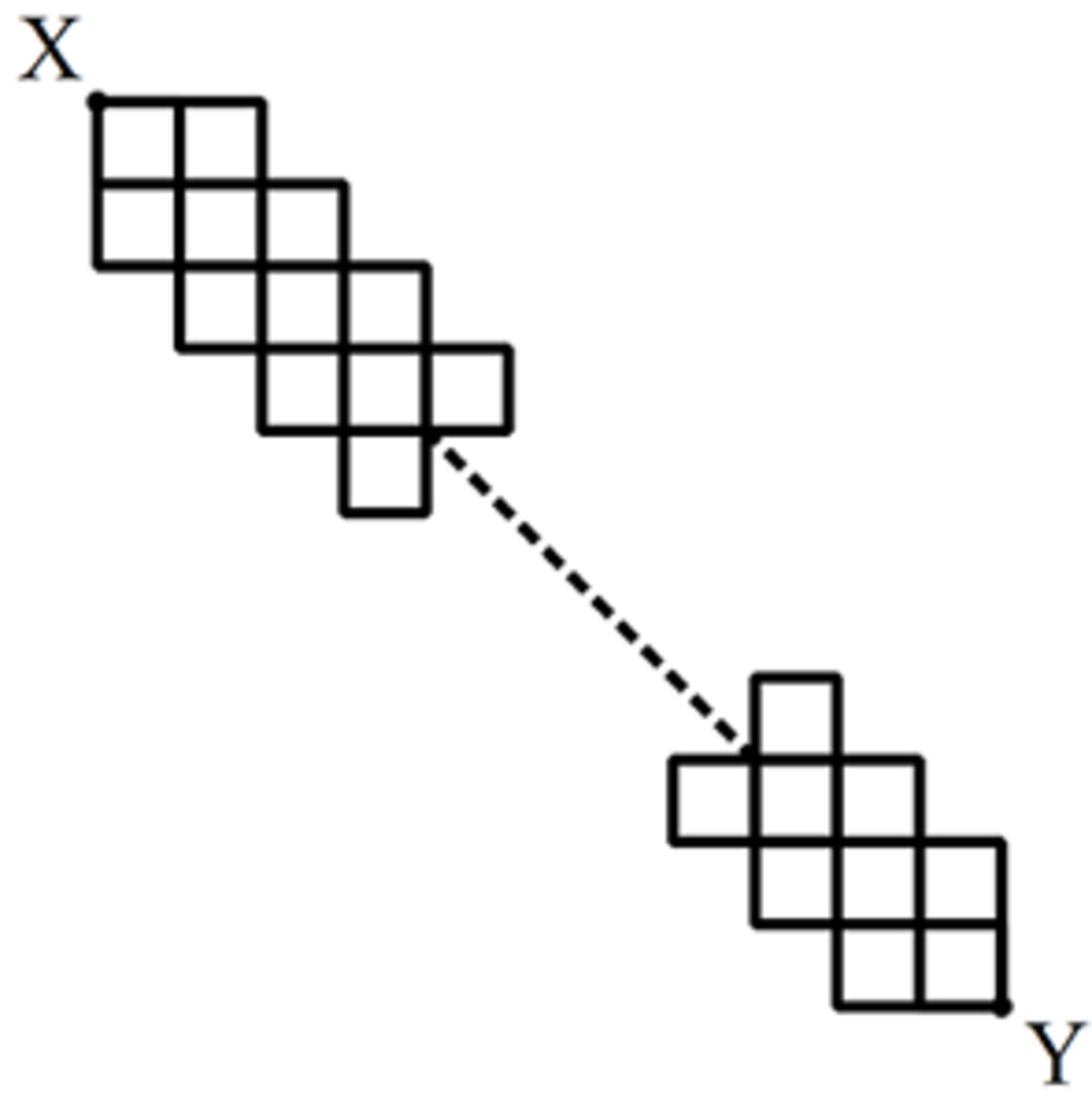
The above consists of n number of 2 × 2 squares such that each adjacent 2 × 2 squares overlap each other on exactly one 1 × 1 square. And I can only move 1 unit down or 1 unit to the right at a time.
Let M n denote the total number paths for me to choose from such that I start the top left point on the top, X til I to move to the bottom right point on the bottom, Y .
Find n → ∞ lim M n M n + 1 .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Not true. M 1 = 6 , M 2 = 1 8 , M 3 = 5 4 , but M 4 = 1 6 8 = 3 M 3 .
Log in to reply
I think you may have made a miscalculation for M 4 . I found it to be 162. Is there something wrong with my logic in my solution?
Log in to reply
Awhhh damn it. I added 6 for nothing. Sorry about that!
Exact same.
Suppose there are 2 x ways of reaching the bottom right point for n number of squares. Then, by symmetry, there are x number of ways to reach the point immediately to the left of the bottom right point and the point immediately to the top of the bottom right point. Now, we add the n + 1 th square. We can draw the diagram as such.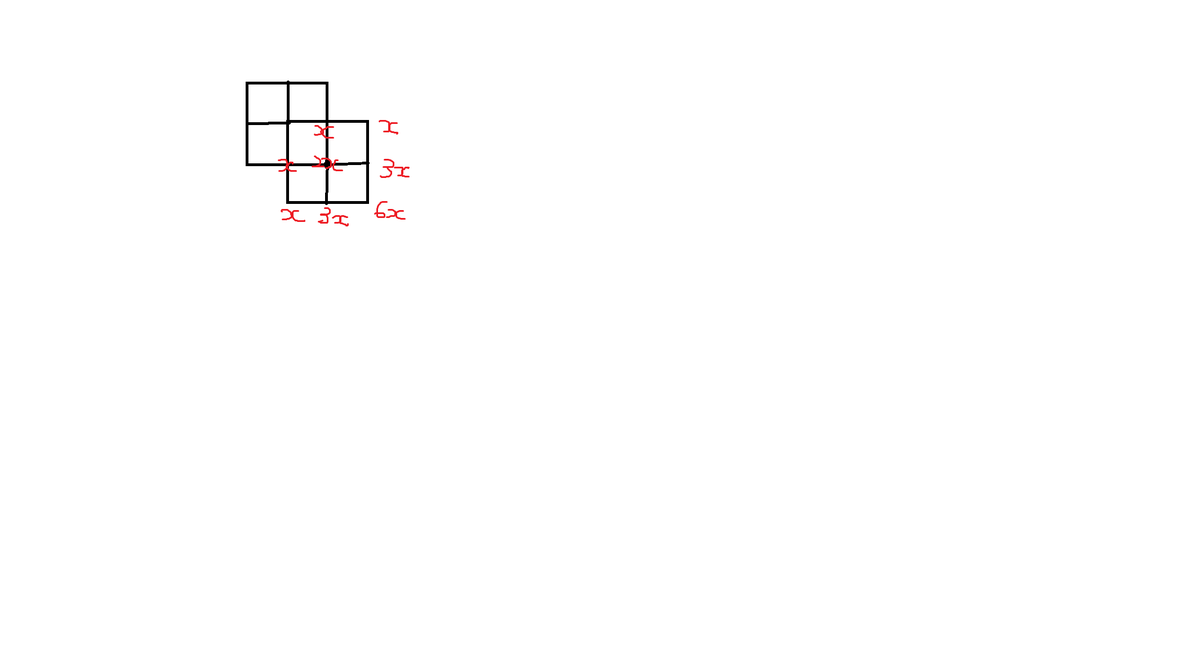
Hence, it follows that M n + 1 = 3 M n , and the answer is 3.