Overload Infinity Transformer?

Electricity and Magnetism Level 5

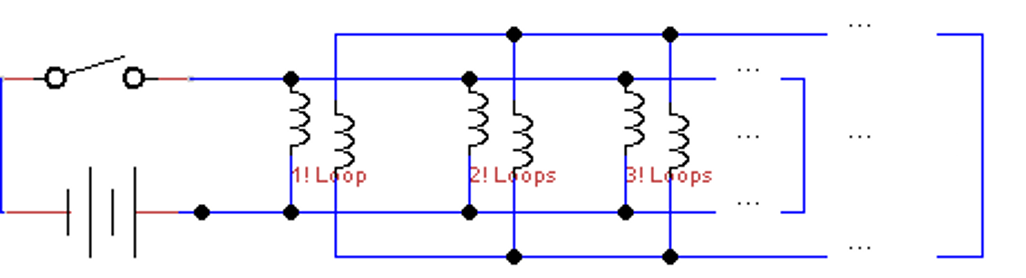
Refer to the figure shown. An E E - V V battery and infinitely many solenoids of 1 ! 1! , 2 ! 2! , 3 ! 3! and so on. The number of loops is connected in parallel. Another circuit has each of the infinite number of corresponding identical solenoids having N N loops and internal resistance R R connected in parallel. This circuit is placed near but not in contact with the former circuit.

In terms of the variables given, determine the total current induced when the switch is closed.

Details and Assumptions :

  • V V is read as Volts, the unit of potential difference.

  • All elements are Ohmic.

E N R ( e − 1 ) \dfrac{E}{NR} (e-1) ∞ \infty N E R ( e − 1 ) \dfrac{NE}{R} (e-1) E R ( e − 1 ) \dfrac{E}{R} (e-1) E N R e \dfrac{E}{NR} e N E R e \dfrac{NE}{R} e N E R e NERe E R \dfrac{E}{R}

Louie Dy by Louie Dy , 24, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Louie Dy
May 4, 2016

One of the equations on transformers is the following:
V 1 N 1 = V 2 N 2 \dfrac{V_1}{N_1} = \dfrac{V_2}{N_2}

By substitution, the transformation for each of the primary n ! n! -loop to secondary N N -loop leads to:

E n ! = V n N \dfrac{E}{n!} = \dfrac{V_n}{N}

V n = N E n ! V_n = \dfrac{NE}{n!}

By Ohm's Law (since the solenoids are Ohmic),

I n = N E n ! R I_n = \dfrac{NE}{n!R}

Then getting the sum:

∑ n = 1 ∞ I n \displaystyle\sum_{n=1}^\infty I_n

∑ n = 1 ∞ N E n ! R \displaystyle\sum_{n=1}^\infty \dfrac{NE}{n!R}

N E R ∑ n = 1 ∞ 1 n ! \dfrac{NE}{R} \displaystyle\sum_{n=1}^\infty \dfrac{1}{n!}

By Maclaurin Series,

N E R ( e − 1 ) \dfrac{NE}{R} (e-1)

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...