Oxford Entrance Exam Problem 5

The reflection of the point ( 1 , 0 ) in the line y = m x has coordinates
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
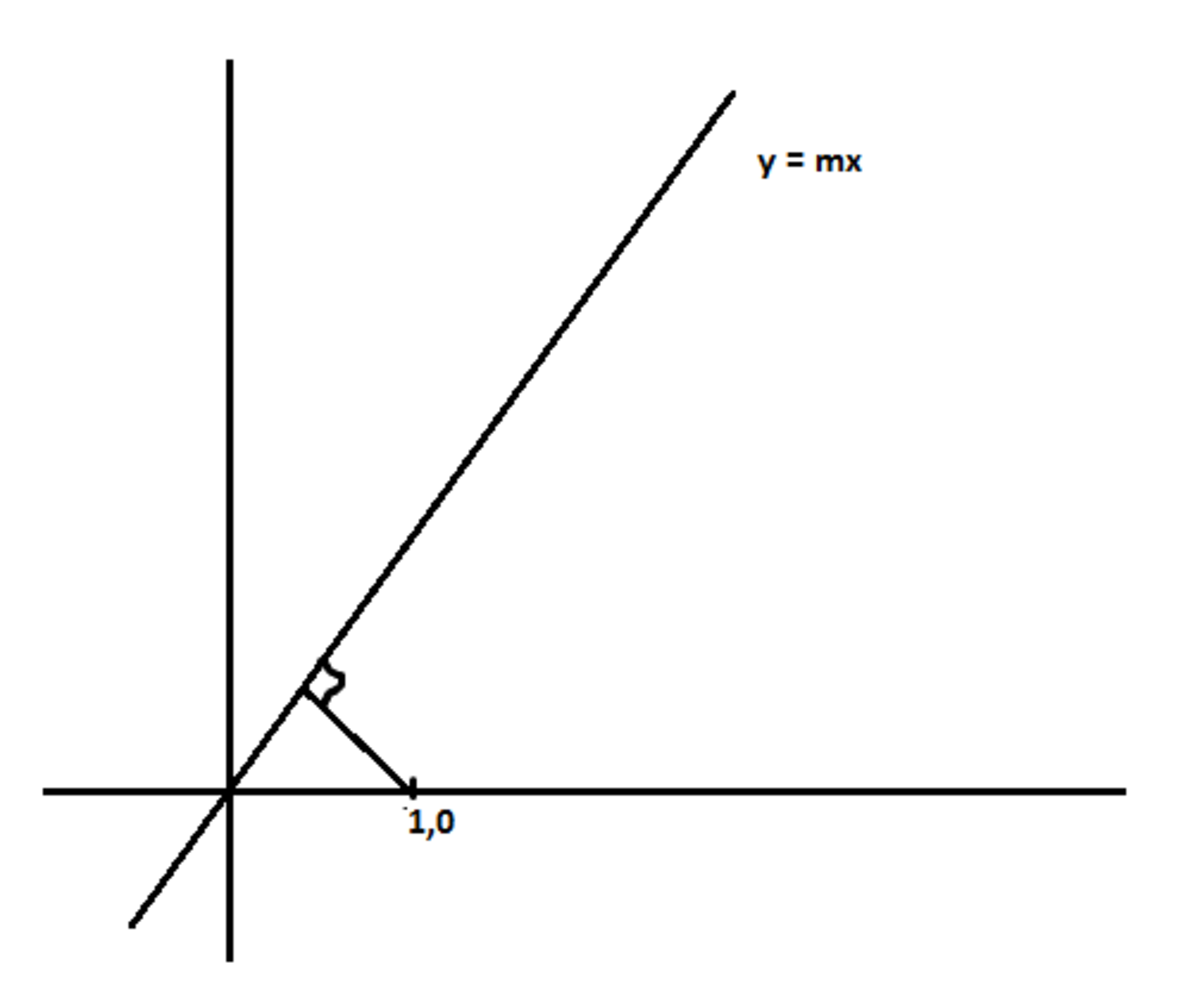
In the above graph drawn, we are constructing a perpendicular line from ( 1 , 0 ) to the line y = m x
Using slope-point formula, the equation of the constructed line would be
y + m x = m 1
Equating the above line and y = m x , we get the point of intersection as ( 1 + m 2 1 , 1 + m 2 m )
The point of intersection is the mid point of the line joining the reflection and the object.
Let the reflection be ( α , β )
Using mid-point formula, we get ( α , β ) = ( 1 + m 2 1 − m 2 , 1 + m 2 2 m )
If you're allowed to use the options, you can rule out all but one pretty quickly. First, let's say the reflected point is in the form ( f ( m ) , g ( m ) ) . Right away, we know that { lim m → ∞ f ( m ) = − 1 lim m → ∞ g ( m ) = 0 This leaves only two possibilities for g ( m ) : 1 + m 2 2 m , m 2 − 1 m . The second option's accompanying f ( m ) has a limit of 1 and not − 1 , leaving one option.
If not, there's a simple geometric approach:
We have that a + m 2 a = 1 so a = m 2 + 1 1 . We now have that the y coordinate is 1 + m 2 2 m .
The x is a little bit trickier, but we can see that it's just a − m 2 a which gives a final result for the x as m 2 + 1 1 − m 2 .